如图所示，圆柱的高为2，底面半径为,AE、DF是圆柱的两条母线，过作圆柱的截面交下底面于.

（1）求证：；

（2）若四边形ABCD是正方形，求证；

（3）在（2）的条件下，求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中，利用由圆柱的性质知：AD平行平面ＢＣＦＥ

又过作圆柱的截面交下底面于.∥ 

又AE、DF是圆柱的两条母线

∥ＤＦ，且ＡＥ＝ＤＦ　　　　　ＡＤ∥ＥＦ

第二问中，由线面垂直得到线线垂直。四边形ABCD是正方形　　又

BC、AE是平面ABE内两条相交直线

 

第三问中，设正方形ABCD的边长为x,则在

在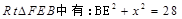 

由（2）可知：为二面角A-BC-E的平面角，所以

证明：（1）由圆柱的性质知：AD平行平面ＢＣＦＥ

又过作圆柱的截面交下底面于.∥ 

又AE、DF是圆柱的两条母线

∥ＤＦ，且ＡＥ＝ＤＦ　　　　　ＡＤ∥ＥＦ 

(2) 四边形ABCD是正方形　　又

BC、AE是平面ABE内两条相交直线

 

(3)设正方形ABCD的边长为x,则在

在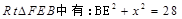 

由（2）可知：为二面角A-BC-E的平面角，所以

 

 下面几种推理是合情推理的是＿＿＿＿＿＿　（填写序号）　

①由圆的性质类比得出球的有关性质；

②由直角三角形、等腰三角形、等边三角形内角和是180°，归纳出所有三角形的内角和都是；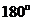

③四边形内角和是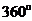，五边形内角和是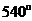，由此得出凸多边形内角和是．

 

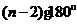下面几种推理是合情推理的是                                          (　　)

①由圆的性质类比出球的有关性质；

②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；

③张军某次考试成绩是100分，由此推出全班同学的成绩都是100分；

④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸多边形内角和是(n－2)·180°.

A．①②                 B．①③

C．①②④              D．②④

下列推理是归纳推理的是(　　)

A．A，B为定点，动点P满足|PA|＋|PB|＝2a>|AB|，则P点的轨迹为椭圆

B．由a₁＝1，a_n＝3n－1，求出S₁，S₂，S₃，猜想出数列的前n项和S_n的表达式

C．由圆x²＋y²＝r²的面积πr²，猜想出椭圆＝1的面积S＝πab

D．利用等差数列的性质推理得到等比数列的相关性质

 

已知等差数列{a_n}的首项为4，公差为4，其前n项和为S_n，则数列 {}的前n项和为（　　）

A．

B．

C．

D．

考点：	数列的求和；等差数列的性质．
专题：	等差数列与等比数列．
分析：	利用等差数列的前n项和即可得出Sn，再利用“裂项求和”即可得出数列 {}的前n项和．
解答：	解：∵Sn=4n+=2n2+2n， ∴． ∴数列 {}的前n项和===． 故选A．
点评：	熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键．