
题目列表(包括答案和解析)
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
(本小题满分16分)
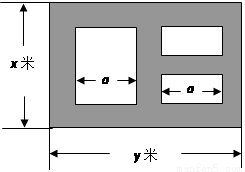
某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米。
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值。
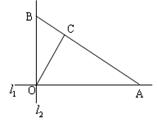
(本题16分)如图,在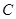 城周边已有两条公路
城周边已有两条公路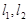 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为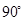 .已知
.已知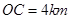 ,
, 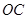 与公路
与公路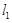 夹角为
夹角为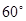 .现规划在公路
.现规划在公路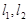 上分别选择
上分别选择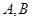 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过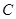 城.设
城.设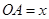
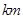 ,
,
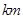 .
.
(1) 求出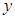 关于
关于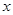 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域;
(2) 试确定点A,B的位置,使△ 的面积最小.
的面积最小.
(本小题满分16分)从数列![]() 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列![]() 的一个子数列.
的一个子数列.
设数列![]() 是一个首项为
是一个首项为![]() 、公差为
、公差为![]()
![]() 的无穷等差数列(即项数有无限项).
的无穷等差数列(即项数有无限项).
(1)若![]() ,
,![]() ,
,![]() 成等比数列,求其公比
成等比数列,求其公比![]() .
.
(2)若![]() ,从数列
,从数列![]() 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为![]() 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若![]() ,从数列
,从数列![]() 中取出第1项、第
中取出第1项、第![]()
![]() 项(设
项(设![]() )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当![]() 为何值时,该数列为
为何值时,该数列为![]() 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com