
题目列表(包括答案和解析)
如图, 是△
是△ 的重心,
的重心, 、
、 分别是边
分别是边 、
、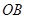 上的动点,且
上的动点,且 、
、 、
、 三点共线.
三点共线.
(1)设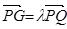 ,将
,将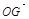 用
用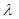 、
、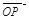 、
、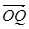 表示;
表示;
(2)设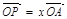 ,
,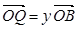 ,证明:
,证明: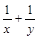 是定值;
是定值;
(3)记△ 与△
与△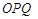 的面积分别为
的面积分别为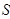 、
、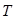 .求
.求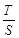 的取值范围.
的取值范围.
(提示: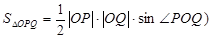
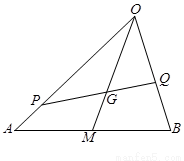
【解析】第一问中利用(1)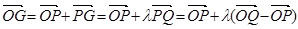
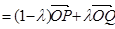
第二问中,由(1),得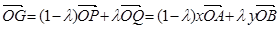 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴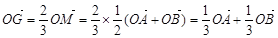
而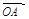 、
、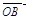 不共线,∴由①、②,得
不共线,∴由①、②,得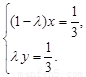
第三问中,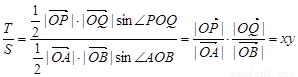
由点 、
、 的定义知
的定义知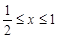 ,
,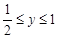 ,
,
且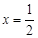 时,
时,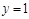 ;
;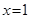 时,
时,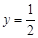 .此时,均有
.此时,均有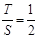 .
.
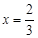 时,
时,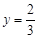 .此时,均有
.此时,均有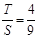 .
.
以下证明: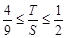 ,结合作差法得到。
,结合作差法得到。
解:(1)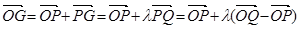
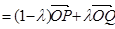 .
.
(2)一方面,由(1),得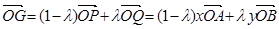 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴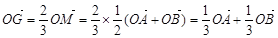 . ②
. ②
而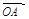 、
、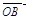 不共线,∴由①、②,得
不共线,∴由①、②,得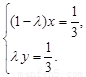
解之,得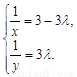 ,∴
,∴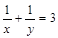 (定值).
(定值).
(3)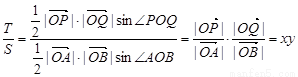 .
.
由点 、
、 的定义知
的定义知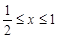 ,
,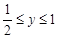 ,
,
且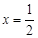 时,
时,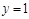 ;
;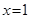 时,
时,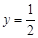 .此时,均有
.此时,均有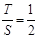 .
.
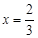 时,
时,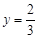 .此时,均有
.此时,均有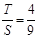 .
.
以下证明: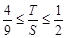 .(法一)由(2)知
.(法一)由(2)知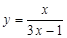 ,
,
∵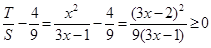 ,∴
,∴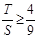 .
.
∵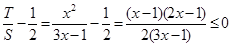 ,∴
,∴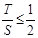 .
.
∴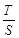 的取值范围
的取值范围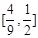
|
| OQ |
| OP |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
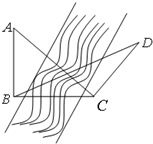 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是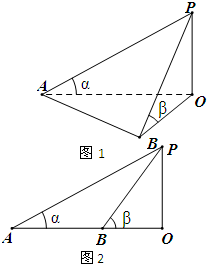 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.| 4 | d |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com