（本小题满分10分）把正整数列按如下规律排列：

  1，    

  2，3，

  4，5，6，7，

  8，9，10，11，12，13，14，15，

  ……

  问：（I）此表第n行的第一个数是多少？

     （II）此表第n行的各个数之和是多少？

是否存在，使得第行起的连续10行的所有数之和为？若存在，求出的值；若不存在，说明理由.

（本小题满分10分）把正整数列按如下规律排列：

  1，    

  2，3，

  4，5，6，7，

  8，9，10，11，12，13，14，15，

  ……

  问：（I）此表第n行的第一个数是多少？

     （II）此表第n行的各个数之和是多少？

是否存在，使得第行起的连续10行的所有数之和为？若存在，求出的值；若不存在，说明理由.

（本小题满分12分）某公司有男职员45名，女职员15名，按照分层抽样的方法组建了一个4人的科研攻关小组。

（1）求某职员被抽到的概率及科研攻关小组中男、女职员的人数；

（2）经过一个月的学习、讨论，这个科研攻关组决定选出两名职员做某项实验，方法是先从小组里选出1名职员做实验，该职员做完后，再从小组内剩下的职员中选一名做实验，求选出的两名职员中恰有一名女职员的概率；

（3）实验结束后，第一次做实验的职员得到的实验数据为68，70，71，72，74，第二次做实验的职员得到的实验数据为69，70，70，72，74，请问哪位职员的实验更稳定？并说明理由。

（本小题满分12分）

某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5； 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。令表示方案实施两年后柑桔产量达到灾前产量的倍数。

（1）写出的分布列；

（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？

（3）不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？

（本小题满分12分）
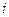某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。令表示方案实施两年后柑桔产量达到灾前产量的倍数。
（1）写出的分布列；
（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？
（3）不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？