
题目列表(包括答案和解析)
翼型降落伞有很好的飞行性能,跳伞运动员可方便地控制转弯等动作.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2其中C1、C2相互影响,可由运动员调节,满足如图乙所示的关系.试求:

(1)图甲中画出了运动员携带翼型伞跳伞后的两条大致运动轨迹,试判断①、②两轨迹中哪条是不可能的,并简要说明理由;
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,试从力平衡的角度证明:tanα=![]() ;
;
(3)某运动员和装备的总质量为70kg,匀速飞行的速度v与地平线的夹角α约20°,tan20°=![]() ,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
(4)若运动员出机舱时飞机距地面的高度为800m,飞机飞行速度为540km/h,降落过程中该运动员和装备损失的机械能ΔE多大?
翼型降落伞有很好的飞行性能,跳伞运动员可方便地控制转弯等动作.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2其中C1、C2相互影响,可由运动员调节,满足如图乙所示的关系.试求:
(1)图甲中画出了运动员携带翼型伞跳伞后的两条大致运动轨迹,试判断①、②两轨迹中哪条是不可能的,并简要说明理由;
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,试从力平衡的角度证明:tanα=![]() ;
;
(3)某运动员和装备的总质量为70kg,匀速飞行的速度v与地平线的夹角α约20°,tan20°=![]() ,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
(4)若运动员出机舱时飞机距地面的高度为800m,飞机飞行速度为540km/h,降落过程中该运动员和装备损失的机械能ΔE多大?
翼型降落伞有很好的飞行性能,跳伞运动员可方便地控制转弯等动作.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2其中C1、C2相互影响,可由运动员调节,满足如图乙所示的关系.试求:

(1)图甲中画出了运动员携带翼型伞跳伞后的两条大致运动轨迹,试判断①、②两轨迹中哪条是不可能的,并简要说明理由;
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,试从力平衡的角度证明:tanα= ;
;
(3)某运动员和装备的总质量为70kg,匀速飞行的速度v与地平线的夹角α约20°,tan20°=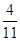 ,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
,匀速飞行的速度v多大?(g取10m/s2,结果保留3位有效数字.)
(4)若运动员出机舱时飞机距地面的高度为800m,飞机飞行速度为540km/h,降落过程中该运动员和装备损失的机械能ΔE多大?
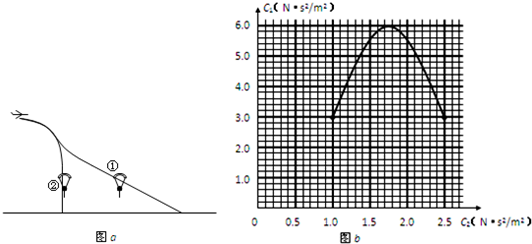
 翼型降落伞有很好的飞行性能.它被看作飞机的机翼,跳伞运动员可方便地控制转弯等动物.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2.其中C1.C2相互影响,可由运动员调节,满足如图b所示的关系.试求:
翼型降落伞有很好的飞行性能.它被看作飞机的机翼,跳伞运动员可方便地控制转弯等动物.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2.其中C1.C2相互影响,可由运动员调节,满足如图b所示的关系.试求:一、1、BC 2、B 3、C 4、AD 5、ACD 6、D 7、ABD 8、C
9、C 10、ACD 11、BD 12、D
二、实验题(本题共2小题共18分)将答案填在横线上或作图和连线
13、(8分)(1)实验装置图中存在的问题有:细线与轨道平面应该平行;---1分
初始时刻,小车应紧靠打点计时器 ---1分
所缺的步骤:调节轨道的倾斜程度,使小车能在轨道上匀速运动为止 ------1分
应该控制的实验条件是M>>m------1分
(2) ---1分
---1分
 ---1分
---1分
 -----2分
-----2分
14、(10分)(1)①_____30.6~30.9 (1分)

②__150____ (1分)
③____?1K (1分)
④ 欧姆调零 (1分)
(2)① B (1分)
② 新电池内阻很小(1分) ③电路图(4分)
三、本大题共四小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
15、(12分)(1)设电子经电压U1加速后的速度为v0,由动能定理
e U1= -0…………………………………………(2分)
-0…………………………………………(2分)
解得  ………………………………..………(2分)
………………………………..………(2分)
(2)电子以速度v0进入偏转电场后,垂直于电场方向做匀速直线运动,沿电场方向做初速度为零的匀加速直线运动。设偏转电场的电场强度为E,电子在偏转电场中运动的时间为t,加速度为a,电子离开偏转电场时的侧移量为y。由牛顿第二定律和运动学公式
t= ……………………………………………..……….(1分)
……………………………………………..……….(1分)
F=ma F=eE E=
a = ……………………………………………(2分)
……………………………………………(2分)
y= ……………………………………………(1分)
……………………………………………(1分)
解得 y= …………………………………………(2分)
…………………………………………(2分)
(3)减小加速电压U1;增大偏转电压U2;……(2分)
16、(13分)(1)(4分)②轨迹不可能存在
①位置,三力可能平衡或三力的合力可能与速度在一直线.,运动员做直线运动
②位置,合力方向与速度方向不可能在一直线,所以不会沿竖直方向做直线运动
②位置F1的方向按图a,理论上是向右,画出向左也不扣分,但是F1F2标错位置要扣分。.
(2)(3分)由①位置的受力分析可知,匀速运动时
F1=mgcos=C1v2……⑴
F2=mgsin=C2v2……⑵
两式消去mg和v得tan=C2/C1
(3)(3分)在图b中过原点作直线
正确得到直线与曲线的交点
C2=2,C1=5.55.5~5.6均正确.
根据F2=mgsin=C2v2或F1=mgcos=C1v2
上两式任取其一.
得v=10.9m/s在10.7~11.0之间均可.
(4)(3分)E=mgH+12 mv02-12 mv2=7010800+12 701502-12 7010.92.J=1.34106 J
 17、(14分)(1)设小环到达b点的速率为v1,因小环在b点恰好与细杆无相互作用力,则有:Eq=qv1B(2分)
17、(14分)(1)设小环到达b点的速率为v1,因小环在b点恰好与细杆无相互作用力,则有:Eq=qv1B(2分)
得 :
: (2分)
(2分)
对小环在ab段的运动过程用动能定理,有:
 (2分)
(2分)
得:W=-6×10-3J(1分)
 (2)小环在cd段做匀速直线运动,且与细杆无相互作用力,则小环受力情况如图所示.
(2)小环在cd段做匀速直线运动,且与细杆无相互作用力,则小环受力情况如图所示.
设小环刚过c点的速度为v2,由几何关系可知,
电场力Eq=mg(1分),w.w.w.k.s.5
u.c.o.m洛伦兹力 (1分)
(1分)
|