
题目列表(包括答案和解析)
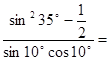
A.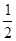 B.
B.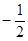 C.
C.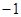 D.1
D.1
 ="( " )
="( " )A. | B. | C. | D.1 |
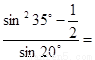 ( )
( )
A.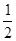 B.
B.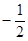 C.
C. D.1
D.1
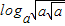 =( )
=( )


![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
一、选择题:
1―5 ACBBD 6―10 BCDAC
二、填空题:
11.60 12. 13.―
13.― 14.
14.
15.2 16. 17.
17.
三、解答题:
18.解:(I)
|