
题目列表(包括答案和解析)
(本小题满分16分)
某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.
规定:每辆自行车的日租金不超过20元,每辆自行车的日租金![]() 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用
元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用![]() 表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得).
表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得).
(1)求函数![]() 的解析式及定义域;
的解析式及定义域;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元? 日净收入最多为多少元?
已知递增等差数列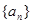 满足:
满足: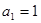 ,且
,且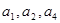 成等比数列.
成等比数列.
(1)求数列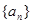 的通项公式
的通项公式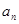 ;
;
(2)若不等式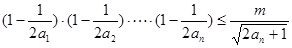 对任意
对任意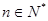 恒成立,试猜想出实数
恒成立,试猜想出实数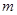 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列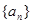 公差为
公差为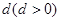 ,
,
由题意可知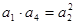 ,即
,即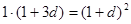 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于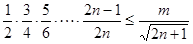 ,利用当
,利用当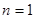 时,
时,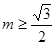 ;当
;当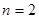 时,
时,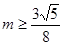 ;而
;而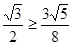 ,所以猜想,
,所以猜想,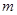 的最小值为
的最小值为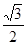 然后加以证明即可。
然后加以证明即可。
解:(1)设数列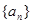 公差为
公差为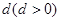 ,由题意可知
,由题意可知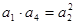 ,即
,即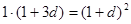 ,
,
解得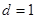 或
或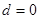 (舍去). …………3分
(舍去). …………3分
所以,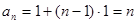 . …………6分
. …………6分
(2)不等式等价于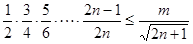 ,
,
当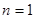 时,
时,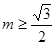 ;当
;当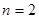 时,
时,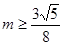 ;
;
而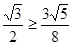 ,所以猜想,
,所以猜想,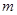 的最小值为
的最小值为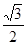 . …………8分
. …………8分
下证不等式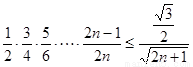 对任意
对任意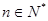 恒成立.
恒成立.
方法一:数学归纳法.
当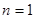 时,
时,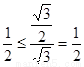 ,成立.
,成立.
假设当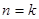 时,不等式
时,不等式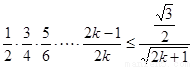 成立,
成立,
当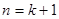 时,
时,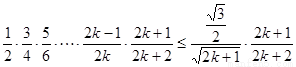 ,
…………10分
,
…………10分
只要证 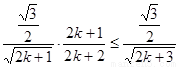 ,只要证
,只要证 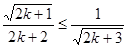 ,
,
只要证 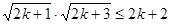 ,只要证
,只要证 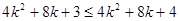 ,
,
只要证 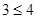 ,显然成立.所以,对任意
,显然成立.所以,对任意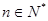 ,不等式
,不等式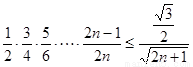 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 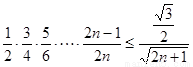
只要证 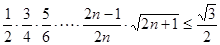 ,
,
设数列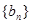 的通项公式
的通项公式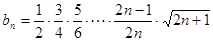 , …………10分
, …………10分
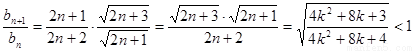 , …………12分
, …………12分
所以对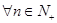 ,都有
,都有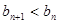 ,可知数列
,可知数列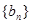 为单调递减数列.
为单调递减数列.
而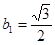 ,所以
,所以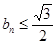 恒成立,
恒成立,
故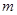 的最小值为
的最小值为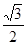 .
.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(I)从袋中随机抽取一个球,将其编号记为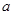 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为 .求关于
.求关于 的一元二次方程
的一元二次方程 有实根的概率;
有实根的概率;
(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域 内的概率.
内的概率.
【解析】第一问利用古典概型概率求解所有的基本事件数共12种,然后利用方程 有实根,则满足△=4a2-4b2≥0,即a2≥b2。,这样求得事件发生的基本事件数为6种,从而得到概率。第二问中,利用所有的基本事件数为16种。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16种。在求解满足
有实根,则满足△=4a2-4b2≥0,即a2≥b2。,这样求得事件发生的基本事件数为6种,从而得到概率。第二问中,利用所有的基本事件数为16种。即基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (3,1)
(3,2) (3,3)
(3,4) (4,1) (4,2) (4,3)
(4,4)共16种。在求解满足 的基本事件数为(1,1) (2,1) (2,2) (3,1) 共4种,结合古典概型求解得到概率。
的基本事件数为(1,1) (2,1) (2,2) (3,1) 共4种,结合古典概型求解得到概率。
(1)基本事件(a,b)有:(1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)共12种。
∵ 有实根, ∴△=4a2-4b2≥0,即a2≥b2。
有实根, ∴△=4a2-4b2≥0,即a2≥b2。
记“ 有实根”为事件A,则A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6种。
有实根”为事件A,则A包含的事件有:(2,1) (3,1)
(3,2) (4,1) (4,2) (4,3) 共6种。
∴PA.=  。 …………………6分
。 …………………6分
(2)基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,4) (4,1) (4,2) (4,3) (4,4)共16种。
记“点P落在区域 内”为事件B,则B包含的事件有:
内”为事件B,则B包含的事件有:
(1,1) (2,1) (2,2) (3,1) 共4种。∴PB.=
已知函数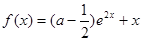 .(
.(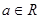 )
)
(1)若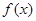 在区间
在区间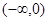 上单调递增,求实数
上单调递增,求实数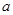 的取值范围;
的取值范围;
(2)若在区间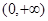 上,函数
上,函数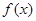 的图象恒在曲线
的图象恒在曲线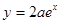 下方,求
下方,求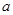 的取值范围.
的取值范围.
【解析】第一问中,首先利用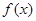 在区间
在区间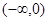 上单调递增,则
上单调递增,则 在区间
在区间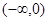 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到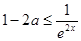 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间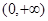 上,函数
上,函数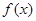 的图象恒在曲线
的图象恒在曲线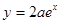 下方等价于
下方等价于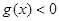 在区间
在区间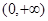 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1)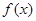 在区间
在区间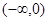 上单调递增,
上单调递增,
则 在区间
在区间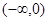 上恒成立. …………3分
上恒成立. …………3分
即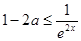 ,而当
,而当 时,
时,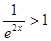 ,故
,故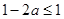 .
…………5分
.
…………5分
所以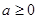 .
…………6分
.
…………6分
(2)令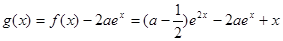 ,定义域为
,定义域为 .
.
在区间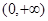 上,函数
上,函数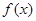 的图象恒在曲线
的图象恒在曲线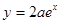 下方等价于
下方等价于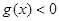 在区间
在区间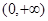 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若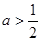 ,令
,令 ,得极值点
,得极值点 ,
,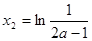 ,
,
当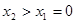 ,即
,即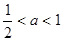 时,在(
时,在(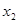 ,+∞)上有
,+∞)上有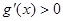 ,此时
,此时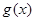 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有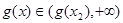 ,不合题意;
,不合题意;
当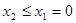 ,即
,即 时,同理可知,
时,同理可知,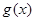 在区间
在区间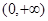 上递增,
上递增,
有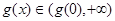 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若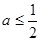 ,则有
,则有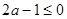 ,此时在区间
,此时在区间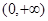 上恒有
上恒有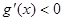 ,从而
,从而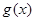 在区间
在区间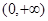 上是减函数;
上是减函数;
要使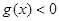 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足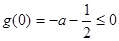
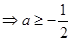 ,
,
由此求得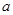 的范围是
的范围是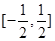 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数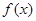 的图象恒在直线
的图象恒在直线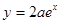 下方.
下方.
某校从参加高三年级第一学期期末考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数,满分为100分),将数学成绩进行分组并根据各组人数制成如下频率分布表:
(Ⅰ)将上面的频率分布表补充完整,并估计本次考试全校85分以上学生的比例;
(Ⅱ)为了帮助成绩差的同学提高数学成绩,学校决定成立“二帮一”小组,即从成绩为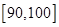 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在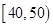 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分,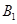 同学成绩为95分,求
同学成绩为95分,求 、
、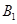 两同学恰好被安排在“二帮一”中同一小组的概率.
两同学恰好被安排在“二帮一”中同一小组的概率.
|
分 组 |
频 数 |
频 率[来源:学_科_网] |
|
[40, 50 ) |
2 |
0.04 |
|
[ 50, 60 ) |
3 |
0.06 |
|
[ 60, 70 ) |
14 |
0.28 |
|
[ 70, 80 ) |
15 |
0.30 |
|
[ 80, 90 ) |
|
|
|
[ 90, 100 ] |
4 |
0.08 |
|
合 计 |
|
|
【解析】第一问利用表格可知第五行以此填入 12 0.24
第七行以此填入 50 1 估计本次全校85分以上学生比例为32%
第二问中,设数学成绩在[90,100]间的四个同学分别用字母B1,B2,B3,B4表示;被帮助的两个同学为A1,A2出现的“二帮一”小组有A1B1B2;A1B1B3;A1B1B4;A1B2B3;A1B2B4;A1B3B4
A2B1B2;A2B1B3;A2B1B4;A2B2B3;A2B2B4;A2B3B4
A1、B1两同学恰好被安排在“二帮一”中同一小组的有 A1B1B2;A1B1B3;A1B1B4
l利用古典概型概率得到。
(Ⅰ)第五行以此填入 12 0.24 ……………2分
第七行以此填入 50 1 ……………4分
估计本次全校85分以上学生比例为32% ……………6分
(Ⅱ)设数学成绩在[90,100]间的四个同学分别用字母B1,B2,B3,B4表示;被帮助的两个同学为A1,A2出现的“二帮一”小组有A1B1B2;A1B1B3;A1B1B4;A1B2B3;A1B2B4;A1B3B4
A2B1B2;A2B1B3;A2B1B4;A2B2B3;A2B2B4;A2B3B4
A1、B1两同学恰好被安排在“二帮一”中同一小组的有 A1B1B2;A1B1B3;A1B1B4
所以 A1、B1两同学恰好被安排在“二帮一”中同一小组的概率为 3 /12 =1 /4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com