
题目列表(包括答案和解析)
((本小题共13分)
若数列 满足
满足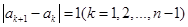 ,数列
,数列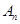 为
为 数列,记
数列,记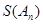 =
=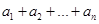 .
.
(Ⅰ)写出一个满足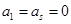 ,且
,且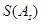 〉0的
〉0的 数列
数列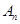 ;
;
(Ⅱ)若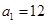 ,n=2000,证明:E数列
,n=2000,证明:E数列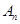 是递增数列的充要条件是
是递增数列的充要条件是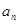 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列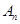 ,使得
,使得 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列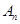 ;如果不存在,说明理由。
;如果不存在,说明理由。
【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(Ⅱ)必要性:因为E数列A5是递增数列,所以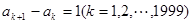 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000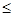 1,a2000—a1000
1,a2000—a1000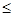 1……a2—a1
1……a2—a1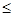 1所以a2000—a
1所以a2000—a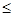 19999,即a2000
19999,即a2000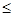 a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故
a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。
.(本小题共13分)函数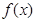 的定义域为R,数列
的定义域为R,数列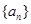 满足
满足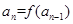 (
(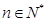 且
且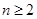 ).
).
(Ⅰ)若数列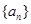 是等差数列,
是等差数列, ,且
,且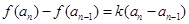 (k为非零常数,
(k为非零常数, 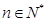 且
且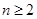 ),求k的值;
),求k的值;
(Ⅱ)若 ,
,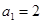 ,
,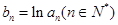 ,数列
,数列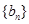 的前n项和为
的前n项和为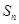 ,对于给定的正整数
,对于给定的正整数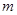 ,如果
,如果 的值与n无关,求k的值.
的值与n无关,求k的值.
 的定义域为R,数列
的定义域为R,数列 满足
满足 (
( 且
且 ).
). 是等差数列,
是等差数列, ,且
,且 (k为非零常数,
(k为非零常数,  且
且 ),求k的值;
),求k的值; ,
, ,
, ,数列
,数列 的前n项和为
的前n项和为 ,对于给定的正整数
,对于给定的正整数 ,如果
,如果 的值与n无关,求k的值.
的值与n无关,求k的值.(本小题满分13分)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持,该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
(本小题满分13分)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持,该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
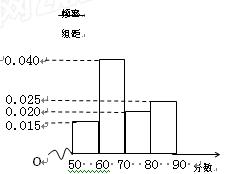
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业的评估分数,得其频率分布直方图如下:
(1)估计该系统所属企业评估得分的中位数及平均分;
(2)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com