练习册

  • 练习册
  • 试题
    某同学按下图所示电路进行实验.实验时该同学把变阻器的触片P移到不同位置时测得各电表的示数如下表所示.将电压表内阻看作无限大.电流表内阻看作零． (1)电路中E.r分别为电源的电动势和内阻.R1.R2.R3为定值电阻.在这五个物理量中.可根据上表中的数据求得的物理量是 , (2)由于电路发生故障.发现两电压表的示数相同.若这种情况的发生是由电阻故障引起的.则可能的故障原因是 ． 【查看更多】

     

    题目列表(包括答案和解析)

    地震、海啸、洪水、森林大火等自然灾害频繁出现，紧急避险常识越来越引起人们的重视．某校为了了解学生对紧急避险常识的了解情况，从高一年级和高二年级各选取100名同学进行紧急避险常识知识竞赛．下图1和图2分别是对高一年级和高二年级参加竞赛的学生成绩按[40，50），[50，60），[60，70），[70，80]分组，得到的频率分布直方图．

    （Ⅰ）分别计算参加这次知识竞赛的两个年级学生的平均成绩；
    （Ⅱ）完成下面2×2列联表，并回答是否有99%的把握认为“两个年级学生对紧急避险常识的了解有差异”？
    成绩小于60分人数 成绩不小于60分人数 合计
    高一年级
    70
    70
    30
    30
    100
    100
    高二年级
    50
    50
    50
    50
    100
    100
    合计
    120
    120
    80
    80
    200
    200
    附：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ．
    临界值表：
    P（K2≥k0） 0.10 0.05 0.010
    k0 2.706 3.841 6.635

    查看答案和解析>>

    某校高三数学竞赛初赛考试后，对考生的成绩进行统计（考生成绩均不低于90分，满分为150分），将成绩按如下方式分成六组，第一组、第二组 、第六组. 下图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人.

    （Ⅰ）求第四和第五组频率，并补全频率分布直方图；

    （Ⅱ）若不低于120分的同学进入决赛，不低于140分的同学为种子选手，完成下面 列联表（即填写空格处的数据），并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.

     

    合计

    参加培训

    5

     

    8

    未参加培训

     

     

     

    合计

     

    4

     

    附：

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

     

     

    查看答案和解析>>

    (本小题满分12分)

    地震、海啸、洪水、森林大火等自然灾害频繁出现，紧急避险常识越来越引起人们的重视．某校为了了解学生对紧急避险常识的了解情况，从七年级和八年级各选取100名同学进行紧急避险常识知识竞赛.下图1和图2分别是对七年级和八年级参加竞赛的学生成绩按，分组，得到的频率分布直方图.

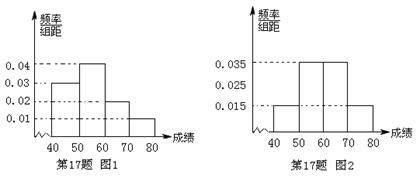
    (Ⅰ)分别计算参加这次知识竞赛的两个年级学生的平均成绩；(注：统计方法中，同一组数据常用该组区间的中点值作为代表)

    (Ⅱ)完成下面列联表，并回答是否有99%的把握认为“两个年级学生对紧急避险常识的了解有差异”？

     

    成绩小于60分人数

    成绩不小于60分人数

    合计

    七年级

     

     

     

    八年级

     

     

     

    合计

     

    附：.

    0.10

    0.05

    0.010

    2.706

    3.841

    6.635

    临界值表：

    查看答案和解析>>

    某学校高三年级有学生1 000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学，
    (Ⅰ)求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
    (Ⅱ)测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如下图：
    (ⅰ)统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170)的中点值为165）作为代表。据此，计算这100名学生身高数据的期望μ及标准差σ（精确到0.1）：
    (ⅱ)若总体服从正态分布，以样本估计总体，据此，估计该年级身高在(158.6，181.4)范围中的学生的人数；
    (Ⅲ)如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
    体育锻炼与身高达标2×2列联表
     
    身高达标
    身高不达标
    总计
    积极参加体育锻炼
    40
     
     
    不积极参加体育锻炼
     
    15
     
    总计
     
     
    100
    (ⅰ)完成上表；
    (ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系？
    参考公式：，
    参考数据：

    查看答案和解析>>


    同步练习册答案