如图.四棱锥S-ABCD的底面是正方形.SD⊥平面ABCD.SD=2..E是SD上的点. (Ⅰ)求证:AC⊥BE, (Ⅱ)求二面角C-AS-D的余弦值. 答案: 连结BD.因为底面ABCD是正方形.所以AC⊥BD. 因为SD⊥平面ABCD.AC平面ABCD. 所以AC⊥SD.---------2分 又因为SDBD=D. 所以AC⊥平面BDS.------4分 因为BE平面BDS. 所以⊥.--------6分 (Ⅱ)因为SD⊥平面ABCD.所以SD⊥CD. 因为底面ABCD是正方形.所以AD⊥CD. 又因为SDAD=D.所以CD⊥平面SAD. 所以CD⊥AS.---------8分 过点D在平面SAD内作DF⊥AS于F.连结CF. 由于.DFCD=D.所以AS⊥平面DCF.所以AS⊥CF. 故∠CFD是二面角C-AS-D的平面角.---------------10分 在Rt△ADS中...可求得. 在Rt△CFD中...可求得. 所以.即二面角C-AS-D的余弦值为.------12分 法二:(Ⅰ)如图以D为原点建立空间直角坐标系.则D.A(.0.0).B(..0).C(0..0).E(0.0.).S. .=.-------3分 ·=2-2+0=0,所以⊥.即AC⊥BE.-------------6分 得=(.0.-2).=(0..-2). 设平面ACS的法向量为. 则由n⊥.n⊥得 即 取.得.-------------------9分 易知平面ASD的一个法向量为=(0,,0). 设二面角C-AS-D的平面角为θ.则. 即二面角C-AS-D的余弦值为.----------------12分 在直三棱柱中.平面.其垂足落在直线上. (Ⅰ)求证:, (Ⅱ)若..为的中点.求三棱锥的体积. 答案: (Ⅰ)三棱柱 为直三棱柱. 平面.又平面. -----------------------------------2分 平面.且平面.. 又平面,平面,.平面.--------------5分 又平面. -----------------------------------6分 (Ⅱ)在直三棱柱 中..平面.其垂足落在直线上, . 在中...,, 在中. -----------------------------------8分 由(Ⅰ)知平面.平面,从而. . 为的中点.-----------------------10分 ---------------------12分 【
查看更多】
题目列表(包括答案和解析)

![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,
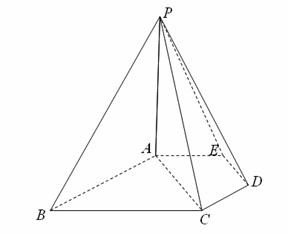
,
![]() ,三角形
,三角形![]() 是等腰三角形.
是等腰三角形.![]() ⊥平面
⊥平面![]() ;
;![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;![]() 的体积.
的体积.