（本小题满分12分）

 (理科)已知数列 {2 ⁿ•a_n} 的前 n 项和 S_n = 9－6n.

 (I)    求数列 {a_n} 的通项公式；

(II)    设 b_n = n·(2－log ₂ )，求数列 { } 的前 n 项和T_n.

（文科）已知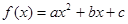，且f(0)=8及f(x+1)－f(x)＝－2x+1。

 (1)求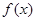的解析式；

 (2)求函数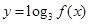的单调递减区间及值域．

（本小题满分12分）

（理科）若，且当时，不等式恒成立，求实数的取值范围。

（文科）已知数列 {2 ⁿ•a_n} 的前 n 项和 S_n = 9－6n.

(I) 求数列 {a_n} 的通项公式；

(II)    设 b_n = n·(2－log ₂ )，求数列 { } 的前 n 项和T_n 。

（本小题满分12分）

根据公安部最新修订的《机动车驾驶证申领和使用规定》：每位驾驶证申领者必须通过《科目一》（理论科目）、《综合科》（驾驶技能加科目一的部分理论）的考试.已知李先生已通过《科目一》的考试，且《科目一》的成绩不受《综合科》的影响，《综合科》三年内有5次预约考试的机会，一旦某次考试通过，便可领取驾驶证，不再参加以后的考试，否则就一直考到第5次为止.设李先生《综合科》每次参加考试通过的概率依次为0.5，0.6，0.7，0.8，0.9．

（1）求在三年内李先生参加驾驶证考试次数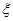的分布列和数学期望；

（2）求李先生在三年内领到驾驶证的概率.

（本小题满分12分）
根据公安部最新修订的《机动车驾驶证申领和使用规定》：每位驾驶证申领者必须通过《科目一》（理论科目）、《综合科》（驾驶技能加科目一的部分理论）的考试.已知李先生已通过《科目一》的考试，且《科目一》的成绩不受《综合科》的影响，《综合科》三年内有5次预约考试的机会，一旦某次考试通过，便可领取驾驶证，不再参加以后的考试，否则就一直考到第5次为止.设李先生《综合科》每次参加考试通过的概率依次为0.5，0.6，0.7，0.8，0.9．
（1）求在三年内李先生参加驾驶证考试次数的分布列和数学期望；
（2）求李先生在三年内领到驾驶证的概率.