练习册

  • 练习册
  • 试题
    33．在同一地点有两个静止的声源.发出声波1和声波2.在同一空间的空气中沿同一方向传播.如图所示为某时刻这两列波的图像.则下列说法中正确的是: A. 波1速度比波2速度大 B. 相对于同一障碍物.波1比波2更容易发生衍射现象 C. 在这两列波传播的方向上.不会产生稳定的干涉现象 D. 在这两列波传播的方向上运动的观察者.听到的这两列波的频率可以相同 用波长为0.51µm的绿光在空气中经双缝在屏上得到干涉条纹.测得相邻两明条纹间距为0.55mm.在水中用红光做上述实验.测得相邻两明条纹间距也为0.55mm.如水的折射率为4/3.求此红光的频率. 选做3-5 【查看更多】

     

    题目列表(包括答案和解析)

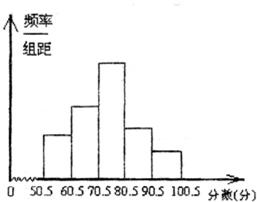    精英家教网某学校举行“科普与环保知识竞赛”，并从中抽取了部分学生的成绩（均为整数），所得数据的分布直方图如图．已知图中从左至右前3个小组的频率之比为1：2：3，第4小组与第5小组的频率分别是0.175和0.075，第2小组的频数为10．
    （Ⅰ）求所抽取学生的总人数，并估计这次竞赛的优秀率（分数大于80分）；
    （Ⅱ）从成绩落在（50.5，60.5）和（90.5，100.5）的学生中任选两人，求他们的成绩在同一组的概率．

    查看答案和解析>>

    某市为了对学生的数理（数学与物理）学习能力进行分析，从10000名学生中随机抽出100位学生的数理综合学习能力等级分数（6分制）作为样本，分数频数分布如下表：
    等级得分 （0，1] （1，2] （2，3] （3，4] （4，5] （5，6]
    人数 3 17 30 30 17 3
    （Ⅰ）如果以能力等级分数大于4分作为良好的标准，从样本中任意抽取2名学生，求恰有1名学生为良好的概率；
    （Ⅱ）统计方法中，同一组数据常用该组区间的中点值（例如区间（1，2]的中点值为1.5）作为代表：
    （ⅰ）据此，计算这100名学生数理学习能力等级分数的期望μ及标准差σ（精确到0.1）；
    （ⅱ） 若总体服从正态分布，以样本估计总体，估计该市这10000名学生中数理学习能力等级在（1.9，4.1）范围内的人数．
    （Ⅲ）从这10000名学生中任意抽取5名同学，他们数学与物理单科学习能力等级分数如下表：

    （ⅰ）请画出右上表数据的散点图；
    （ⅱ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
    y
    =bx+a    （附参考数据：
    		129
    ≈11.4    ）

    查看答案和解析>>

    下面有5个命题：
    ①分针每小时旋转2π弧度；  ②函数f(x)=
    sinx
    1+cosx
    是奇函数；
    ③若
    OA
    =x
    OB
    +y
    OC
    ，且x+y=1，则A，B，C三点共线；
    ④在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点；
    ⑤在△ABC中，若sinA=sinB，则A=B．
    其中，真命题的编号是
    ②③⑤
    ②③⑤
    （写出所有真命题的编号）

    查看答案和解析>>

    下面有5个命题：
    ①分针每小时旋转2π弧度；
    ②若
    OA
    =x
    OB
    +y
    OC
    ，且x+y=1，则A，B，C三点共线；
    ③在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点；
    ④函数f(x)=
    sinx
    1+cosx
    是奇函数；
    ⑤在△ABC中，若sinA=sinB，则A=B．
    其中，真命题的编号是
     
    （写出所有真命题的编号）

    查看答案和解析>>

    已知非零向量
    OA
    、
    OB
    、
    OC
    、
    OD
    满足：
    OA
    =α
    OB
    +β
    OC
    +γ
    OD
    (α，β，γ∈R)    ，B、C、D为不共线三点，给出下列命题：
    ①若α=
    3
    2
    ，β=
    1
    2
    ，γ=-1    ，则A、B、C、D四点在同一平面上；
    ②当α＞0，β＞0，γ=
    		2
    时，若|
    OA
    |=
    		3
    ，|
    OB
    |=|
    OC
    |=|
    OD
    |=1    ，＜
    OB
    ，
    OC
    ＞=
    5π
    6
    ，＜
    OD
    ，
    OB
    ＞=＜
    OD
    ，
    OC
    ＞=
    π
    2
    ，则α+β的最大值为
    		6
    -
    		2
    ；
    ③已知正项等差数列an（n∈N*），若α=a2，β=a2009，γ=0，且A、B、C三点共线，但O点不在直线BC上，则
    1
    a3
    +
    4
    a2008
    的最小值为9；
    ④若α+β=1（αβ≠0），γ=0，则A、B、C三点共线且A分
    BC
    所成的比λ一定为
    α
    β
    ．
    其中你认为正确的所有命题的序号是
     
    ．

    查看答案和解析>>


    同步练习册答案