已知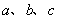是互不相等的非零实数.用反证法证明三个方程，

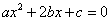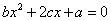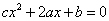，至少有一个方程有两个相异实根.

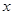已知是互不相等的非零实数，求证：由确定的三条抛物线至少有一条与轴有两个不同的交点.

【解析】本试题主要是考查了运用反证法思想，对于正面解决难的问题的运用。

已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax²+2bx+c=0，bx²+2cx+a=0，cx²+2ax+b=0至少有一个方程有两个相异实根.

【解析】本试题主要考查了二次方程根的问题的综合运用。运用反证法思想进行证明。

先反设，然后推理论证，最后退出矛盾。证明：假设三个方程中都没有两个相异实根，

则Δ₁=4b²－4ac≤0，Δ₂=4c²－4ab≤0，Δ₃=4a²－4bc≤0

相加有a²－2ab+b²+b²－2bc+c²+c²－2ac+a²≤0，

（a－b）²+（b－c）²+（c－a）²≤0.显然不成立。

证明：假设三个方程中都没有两个相异实根，

则Δ₁=4b²－4ac≤0，Δ₂=4c²－4ab≤0，Δ₃=4a²－4bc≤0.

相加有a²－2ab+b²+b²－2bc+c²+c²－2ac+a²≤0，

（a－b）²+（b－c）²+（c－a）²≤0.                                      ①

由题意a、b、c互不相等，∴①式不能成立.

∴假设不成立，即三个方程中至少有一个方程有两个相异实根.

1.         已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax²+2bx+c=0，bx²+2cx+a=0，cx²+2ax+b=0至少有一个方程有两个相异实根，应假设成（    ）

A．三个方程都没有两个相异实根            B．一个方程没有两个相异实根

C．至多两个方程没有两个相异实根          D．三个方程不都没有两个相异实根