设数列满足. (Ⅰ)求数列的通项公式: (Ⅱ)令.求数列的前n项和. [答案] 解: (I)由已知.当时. 而 所以数列的通项公式为 (II)由 可知 则. 如圈.己知四棱锥P-ABCD的底面为等腰梯形.AB∥CD,⊥BD垂足为H,PH是四棱锥的高.E为AD中点. (Ⅰ)证明:PE⊥BC (Ⅱ)若==60°.求直线PA与平面PEH所成角的正弦值. [答案] 解: (I)以为原点...分别为轴.线段的长为单位长度.建立坐标系如图所示. 设 则 可得 ∵ ∴ (II)由已知条件可得.则 ∴ 设是平面的法向量 则 ∴ 因此可以取 可得 ∴直线和平面所成角的正弦值为 为调查某地区老年人是否需要志愿者提供帮助.用简单随机抽样方法从该地区调查了500位老年人.结果如下: (Ⅰ)估计该地区老年人中.需要志愿者提供帮助的老年人的比例, (Ⅱ)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关? 的结论.能否提出更好的调查方法来估计该地区的老年人中.需要志愿者提供帮助的老年人的比例?说明理由. [答案] 解: (I)调查的500位老年人中有70位需要志愿者提供帮助.因此该地区老年人中.需要帮助的老年人的比例估计值为 (II) ∵9.967>6.635.∴有99%的把握认为该地区的老年人是否需要帮助与性别有关 的结论可知.该地区老年人是否需要帮助与性别有关.并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异.因此在调查时.先确定该地区老年人中男.女的比例.再把老年人分成男.女两层并采用分层抽样的方法比采用简单随机抽样方法更好. 设分别是椭圆E:的左.右焦点.过斜率为1的直线l与E 相较于A,B两点.且,,成等差数列. (Ⅰ)求E的离心率, 满足,求E的方程. [答案] 解: 由椭圆定义知.又 得 的方程为.其中 设.则两点坐标满足方程组 化简得 则. 因为直线斜率为1.所以 得 ∴ ∴的离心率 (II)设中点为.由(I)知 . 由得 得 ∴. ∴轨迹的方程为 设函数f(x)=. 的单调区间; ≥0.求a的取值范围. [答案] 解: (I)时.. 当时..当时. 故在上单调递减.在单调递增 (II) 由(I)可知.当且仅当时等号成立.故 ∴当.即时.. ∴当时. 由可得 则当时. ∴当时..而 ∴当时. 综上得的取值范围为 请考生在第三题中任选一题做答.如果多做.则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑. (22) 选修4-1,几何证明选讲 如图.已知圆上的弧=,过C点的圆的切线与BA的延长线交于E点.证明: (Ⅰ)=; (Ⅱ); [答案] 解: (I)∵ 又∵与圆相切于点.∴ ∴ (II)∵. ∴△相似于△ 故 即 (23) 选修4-4;坐标系与参数方程 已知直线: .圆: (为参数). (Ⅰ)当=时.求与的交点坐标, (Ⅱ)过坐标原点O作的垂线.垂足为A,P为OA的中点.当变化时.求P点轨迹的参数方程.并指出它是什么曲线; [答案] 解: (I)当时.的普通方程为.的普通方程为 联立方程组 解得与的交点为. (II)的普通方程为 A点坐标为 ∴当变化时.点轨迹的参数方程为 (为参数) 点轨迹的普通方程为 故点轨迹是圆心为.半径为的圆 选修4-5,不等式选讲 设函数f(x)= 的图像, ≤ax的解集非空.求a的取值范围. [答案] 解: (I)由于 则函数的图像如图所示 (II)由函数与函数的图像可知.当且仅当或时.函数 与函数的图像有交点.故不等式的解集非空时.的取值范围 为 【
查看更多】
题目列表(包括答案和解析)
(本小题满分l2分)
设数列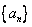 满足
满足 ,
,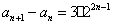
(Ⅰ)求数列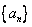 的通项公式:
的通项公式:
(Ⅱ)令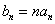 ,求数列
,求数列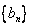 的前n项和
的前n项和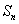 .
.
查看答案和解析>>

![]() 满足
满足![]() ,
,![]()
![]() 的通项公式:
的通项公式:![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.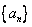 满足
满足 ,
,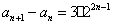
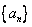 的通项公式:
的通项公式: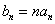 ,求数列
,求数列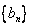 的前n项和
的前n项和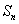 .
.![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]()
![]() =
=![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;![]() 满足
满足![]()
![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]()
![]() =
=![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;![]() 满足
满足![]()
![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.