
题目列表(包括答案和解析)
(本题满分12分)阅读下列材料,解决数学问题.圆锥曲线具有非常漂亮的光学性质,被人们广泛地应用于各种设计之中,比如椭圆镜面用来制作电影放映机的聚光灯,抛物面用来制作探照灯等,它们的截面分别是椭圆和抛物线.双曲线也具有非常好的光学性质,从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是发散的,它们好像是从另一个焦点射出的一样,如图(1)所示.反比例函数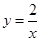 的图像是以直线
的图像是以直线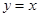 为轴,以坐标轴为渐近线的等轴双曲线,记作C.
为轴,以坐标轴为渐近线的等轴双曲线,记作C.
(Ⅰ)求曲线C的离心率及焦点坐标;
(Ⅱ)如图(2),从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直,求入射光线的方程.
(1) (2)
(2) 
(本题满分12分) 已知mod(a,b)是一个函数,它的意义指的是整数 除以整数
除以整数 所得的余数。下面请你阅读下列在Scilab环境下编写的程序:
所得的余数。下面请你阅读下列在Scilab环境下编写的程序:
S=0;
for i=1:1:100
if mod(i,2)==1
S=S+i^2;
else
S=S-i^2;
end;
end;
print(%io(2),S)
回答下列问题:(1)此程序中包括了哪些基本算法语句?
(2)画出此算法对应的程序框图;
(3)在Scilab环境下用while语句重新设计此程序。
(本题满分12分)如图所示,某市政府决定在以政府大楼 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径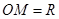 ,
,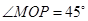 ,
,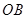 与
与 之间的夹角为
之间的夹角为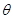 .
.
(1)将图书馆底面矩形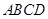 的面积
的面积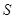 表示成
表示成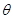 的函数.
的函数.
(2)若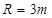 ,求当
,求当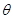 为何值时,矩形
为何值时,矩形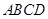 的面积
的面积 有最大值?
有最大值?
其最大值是多少?

(本题满分12分)对任意正整数![]() ,设计一个程序求
,设计一个程序求![]() 的值.
的值.
(本题满分12分)
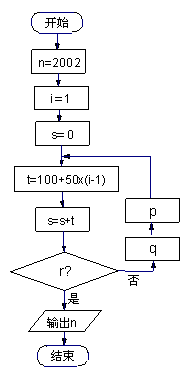
某地区有荒山2200亩,从2002年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.
(1)若所植树全部成活,则到哪一年可以将荒山全部绿化?
(2)右图是某同学设计的解决问题(1)的程序框图,则框图中p,q,r处应填上什么条件?
(3)若每亩所植树苗木材量为2立方米,每年树木木材量的自然增长率为20%,那么到全部绿化后的那一年年底,该山木材总量是多少?(精确到1立方米, ![]() )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com