
题目列表(包括答案和解析)
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合 计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合 计 | 20 |
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
|
|
数学成绩优秀 |
数学成绩不优秀 |
合 计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
参考数据:
假设有两个分类变量 和
和 ,它们的值域分别为
,它们的值域分别为 和
和 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:
|
|
|
|
合计 |
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
则随机变量 ,其中
,其中 为样本容量;
为样本容量;
②独立检验随机变量 的临界值参考表:
的临界值参考表:
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
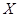 和
和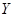 ,它们的值域分别为
,它们的值域分别为 和
和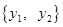 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 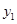 | 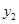 | 合计 |
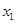 | 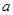 |  | 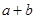 |
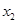 |  | 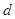 | 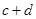 |
| 合计 | 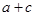 | 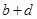 |  |
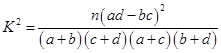 ,其中
,其中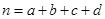 为样本容量;
为样本容量;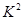 的临界值参考表:
的临界值参考表: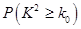 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合 计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合 计 | 20 |
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1)根据上表完成下面的2×2列联表(单位:人): | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 参考数据: ①假设有两个分类变量X和Y它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联 表)为: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
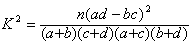 ,其中n=a+b+c+d为样本容量; ,其中n=a+b+c+d为样本容量; ②独立在检验随机变量K2的临界值参考表: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com