
题目列表(包括答案和解析)
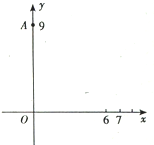 在如图所示的直角坐标系中,一运动物体经过点A(0,9),其轨迹方程为y=ax2+c(a<0),区间D:(6,7)为x轴上的给定区间,为使此物落在区间D内,a的取值范围是
在如图所示的直角坐标系中,一运动物体经过点A(0,9),其轨迹方程为y=ax2+c(a<0),区间D:(6,7)为x轴上的给定区间,为使此物落在区间D内,a的取值范围是| 1 |
| 4 |
| 9 |
| 49 |
| 1 |
| 4 |
| 9 |
| 49 |
 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k,4k+2],k∈z [4k,4k+2],k∈z |
| 递减区间 | [4k-2,4k],k∈z [4k-2,4k],k∈z | |
| 零点 | x=4k,k∈z x=4k,k∈z | |
 如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=
如图所示,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上二点P的位置在(0,0),圆在x轴上沿正向滚动,则当圆滚动到圆心位于(2,1)时线段OP与初始单位圆的交点为M,则|OM|=| 2-2cos2 | ||
|
| 2-2cos2 | ||
|
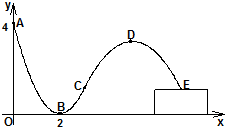 轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米. 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com