题目列表(包括答案和解析)
已知函数f(x)＝ax－lnx＋1(a∈R)，g(x)＝xe1－x．
(Ⅰ)求函数g(x)在区间(0，e]上的值域；
(Ⅱ)是否存在实数a，对任意给定的x0∈(0，e]，在区间[1，e]上都存在两个不同的xi(i＝1，2)，使得f(xi)＝g(x0)成立．若存在，求出a的取值范围；若不存在，请说明理由；
(Ⅲ)
给出如下定义：对于函数y＝F(x)图象上任意不同的两点A(x1，y1)，B(x2，my2)，如果对于函数y＝F(x)图象上的点M(x0，y0)(其中
总能使得F(x1)－f(x2)＝
(x0)(x1－x2)成立，则称函数具备性质“L”，试判断函数f(x)是不是具备性质“L”，并说明理由．
定义：如果数列{an}的任意连续三项均能构成一个三角形的三边长，则称{an}为“三角形”数列．对于“三角形”数列{an}，如果函数y＝f(x)使得bn＝f(an)仍为一个“三角形”数列，则称y＝f(x)是数列{an}的“保三角形函数”，(n∈N*)．
(1)已知{an}是首项为2，公差为1的等差数列，若f(x)＝kx，(k＞1)是数列{an}的“保三角形函数”，求k的取值范围；
(2)已知数列{cn}的首项为2010，Sn是数列{cn}的前n项和，且满足4Sn+1－3Sn＝8040，证明{cn}是“三角形”数列；
(3)若g(x)＝lgx是(2)中数列{cn}的“保三角形函数”，问数列{cn}最多有多少项．
已知定义在区间
上的函数y＝f（x）的图象关于直线
对称，当
时，函数f（x）＝sinx．
（1）求
，
的值；
（2）求y＝f（x）的函数表达式；
（3）如果关于x的方程f（x）＝a有解，那么将方程在a取某一确定值时所求得的所有解的和记为Ma，求Ma的所有可能取值及相对应的a的取值范围．
(12分)如图所示：图1是定义在R上的二次函数f(x)的部分图象，图2是函数g(x)＝loga(x＋b)的部分图象．
(1)分别求出函数f(x)和g(x)的解析式；
(2)如果函数y＝g(f(x))在区间[1，m)上单调递减，求m的取值范围．
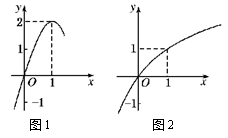如图所示：图1是定义在R上的二次函数f(x)的部分图象，图2是函数g(x)＝loga(x＋b)的部分图象．
⑴分别求出函数f(x)和g(x)的解析式；
⑵如果函数y＝g(f(x))在区间[1，m)上单调递减，求m的取值范围．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com