
题目列表(包括答案和解析)
如图所示,已知正方形ABCD的边长为2,AC∩BD=O,将正方形ABCD沿对角线BD折起,得到三棱锥A—BCD。
(1)求证:平面AOC⊥平面BCD;
(2)若三棱锥A—BCD的体积为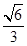 ,求AC的长。
,求AC的长。

【解析】本试题主要是考查立体几何中垂直的证明,以及利用线面的垂直的判定定理和性质定理求解三棱锥的体积,得到AC的长度。
由平面与平面垂直的判定定理知如果m为平面α内的
一条直线,![]() ,则
,则![]() ,反过来则不一定.所以“
,反过来则不一定.所以“![]() ”是“
”是“![]() ”的必要不充分条件. w.w.w.k.s.5.u.c.o.m
”的必要不充分条件. w.w.w.k.s.5.u.c.o.m ![]()
![]()
答案:B.
【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且 .
.
(Ⅰ)求证:CN∥平面AMB1;
(Ⅱ)求证: B1M⊥平面AMG.

【解析】本试题主要是考查了立体几何汇总线面的位置关系的运用。第一问中,要证CN∥平面AMB1;,只需要确定一条直线CN∥MP,既可以得到证明
第二问中,∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,得到线线垂直,B1M⊥AG,结合线面垂直的判定定理和性质定理,可以得证。
解:(Ⅰ)设AB1 的中点为P,连结NP、MP ………………1分


 ∵CM
∵CM  ,NP
,NP  ,∴CM
NP, …………2分
,∴CM
NP, …………2分
∴CNPM是平行四边形,∴CN∥MP …………………………3分
∵CN 平面AMB1,MP奂 平面AMB1,∴CN∥平面AMB1…4分
(Ⅱ)∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,
∵AG⊥BC,∴AG⊥平面CC1 B1 B,∴B1M⊥AG………………6分
∵CC1⊥平面ABC,平面A1B1C1∥平面ABC,∴CC1⊥AC,CC1⊥B1 C,
设:AC=2a,则
 …………………………8分
…………………………8分
同理, …………………………………9分
…………………………………9分
∵ BB1∥CC1,∴BB1⊥平面ABC,∴BB1⊥AB,

 ………………………………10分
………………………………10分

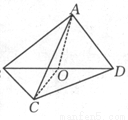
已知平面四边形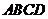 的对角线
的对角线 交于点
交于点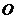 ,
,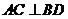 ,且
,且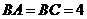 ,
,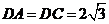 ,
,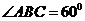 .现沿对角线
.现沿对角线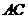 将三角形
将三角形 翻折,使得平面
翻折,使得平面 平面
平面 .翻折后:
(Ⅰ)证明:
.翻折后:
(Ⅰ)证明: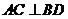 ;(Ⅱ)记
;(Ⅱ)记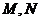 分别为
分别为 的中点.①求二面角
的中点.①求二面角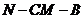 大小的余弦值;
②求点
大小的余弦值;
②求点 到平面
到平面 的距离
的距离

【解析】本试题主要考查了空间中点、线、面的位置关系的综合运用。以及线线垂直和二面角的求解的立体几何试题运用。
已知平面四边形 的对角线
的对角线 交于点
交于点 ,
,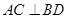 ,且
,且 ,
, ,
,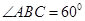 .现沿对角线
.现沿对角线 将三角形
将三角形 翻折,使得平面
翻折,使得平面 平面
平面 .翻折后:
(Ⅰ)证明:
.翻折后:
(Ⅰ)证明: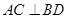 ;(Ⅱ)记
;(Ⅱ)记 分别为
分别为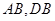 的中点.①求二面角
的中点.①求二面角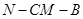 大小的余弦值;
②求点
大小的余弦值;
②求点 到平面
到平面 的距离
的距离
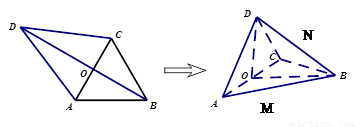

【解析】本试题主要考查了空间中点、线、面的位置关系的综合运用。以及线线垂直和二面角的求解的立体几何试题运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com