(本小题满分12分)

为了解某社区家庭的月均用水量（单位：吨），现从该社区随机抽查户，获得每户某年的月均用水量，并制作了频率分布表和频率分布直方图（如图）.

（Ⅰ）分别求出频率分布表中的值，并估计该社区家庭月均用水量不超过吨的频率；

（Ⅱ）设、、是户月均用水量为的居民代表，、是户月均用水量为的居民代表. 现从这五位居民代表中任选两人参加水价论证会，请列举出所有不同的选法，并求居民代表、至少有一人被选中的概率．

 (本题满分12分)

为调查某工厂工人生产某种产品的能力，随机抽查了一些工人某天生产产品的数量，产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示，保存中不慎丢失一些数据，但已知第一组 （[45,55) ]有4人；

（Ⅰ）求被抽查的工人总人数n及图中所示m为多少；

（Ⅱ）求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。

（本小题满分12分）

为了研究某高校大学新生学生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列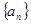的前四项，后6组的频数从左到右依次是等差数列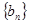的前六项．

   （I）求等比数列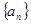的通项公式;

   （II）求等差数列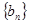的通项公式；

   （III）若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率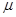的大小.

（本小题满分12分）

某园林局对1000株树木的生长情况进行调查，其中杉树 600株，槐树400株 .现用分层抽样方法从这1000株树木中随机抽取100株，杉树与槐树的树干周长（单位：cm）的抽查结果如下表：

 (I)求，值及估计槐树树干周长的众数；

（Ⅱ）如果杉树的树干周长超过60cm就可以砍伐，请估计该片园林可以砍伐的杉树有多少株？

（Ⅲ）树干周长在30cm到40cm之间的4株槐树有1株患虫害，现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.

（本小题满分12分）为了了解2011年某校高三学生的视力情况，随机抽查了一部分学生视力，将调查结果分组，分组区间为（3.9，4.2]，（4.2，4.5]，… ，（5.1，5.4].经过数据处理，得到如下频率分布表：

（I）求频率分布表中未知量n,x,y,z的值；

（II）从样本中视力在（3.9，4.2]和（5.1，5.4]的所有同学中随机抽取两人，求两人的视力差的绝对值低于0.5的概率．