如图所示.用水培法栽培某植物.请回答下列问题: (1)若要使该植物正常生长.需向水中添加哪些物质? (2)若给水中持续加入大量NaNO3.则会出现何种后果? (3)若持续加入适量的NaNO3.又——青夏教育精英家教网—

如图所示.用水培法栽培某植物.请回答下列问题: (1)若要使该植物正常生长.需向水中添加哪些物质? (2)若给水中持续加入大量NaNO3.则会出现何种后果? (3)若持续加入适量的NaNO3.又会出现什么结果.叶片的颜色会有什么变化?为什么? (4)将叶片x暴露在放射性同位素标记为14CO2中数小时.然后将叶片Ⅰ.Ⅱ和组织Ⅲ.Ⅳ分别切下来.可以预期.在何种组织中测出放射性标记的有机物. A.只有叶片Ⅰ B.只有叶片Ⅰ和Ⅱ C.只有Ⅲ和Ⅳ两部分 D.Ⅰ.Ⅱ.Ⅲ.Ⅳ的所有组织 (5)上题中检测组织中放射性的方法通常称为: A.x射线衍射技术 B.荧光显微技术 C.小型放射性探测器 D.放射自显影术 (6)若要使该植物有最大的净生产量.以下哪些措施正确. ①长光照.短黑暗 ②长黑暗.短光照 ③恒温25℃ ④白昼25℃.夜间15℃ ⑤白昼15℃.夜间25℃ (7)1939年希尔将分离出的叶绿体加到草酸铁溶液中.经过光照后放出O2.同时草酸铁盐被还原成草酸亚铁盐4Fe3++2H2O 4Fe2++4H++O2. 请问希尔实验的重要意义是什么?在光合作用中[H]的有何作用?呼吸作用中[H]又有何作用? 【查看更多】

题目列表(包括答案和解析)

本题共有2个小题，第1小题满分7分，第2小题满分7分．

如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用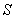平方米塑料片制成圆柱的侧面和下底面（不安装上底面）．

（1）当圆柱底面半径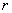取何值时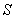，取得最大值？并求出该最大值（结果精确到0.01平方米）;

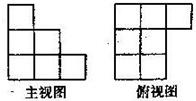（2）若要制作一个如图放置的，底面半径为0.3米的灯笼，请作出用于灯笼的三视图（作图时，不需考虑骨架等因素）．

查看答案和解析>>

用单位正方体搭几何体，使它的主视图和俯视图如图所示，则符合条件的几何体体积的最小值与最大值分别是（　　）

A．9，13

B．7，16

C．10，15

D．10，16

查看答案和解析>>

前不久，省社科院发布了2013年度“安徽城市居民幸福排行榜”，芜湖成为本年度安徽最“幸福城”．随后，师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：
（Ⅰ）指出这组数据的众数和中位数；
（Ⅱ）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”，若幸福度低于7.5分，则称该人的幸福度为“不幸福”．现从这16人中感到“极幸福”和“不幸福”的调查人里随机选取2人，恰有1人是“极幸福”的概率．

查看答案和解析>>

2、用小立方体搭一个几何体，使得它的主视图和俯视图如图所示．这样的几何体需要的小立方块最少与最多分别是（　　）