题目列表(包括答案和解析)
设f(x)，g(x)都是定义在R上的单调函数，有如下四个命题：
①若f(x)单调递增，g(x)单调递增，则f(x)·g(x)单调递增；
②若f(x)单调递增，g(x)单调递减，则f(x)－g(x)单调递增；
③若f(x)单调递减，g(x)单调递增，则f(x)－g(x)单调递减；
④若f(x)单调递增，g(x)单调递减，则f(x)·g(x)单调递减．其中正确命题个数为
A．1
B．2
C．3
D．4
设f1(x)＝x2－b，f2(x)＝
(a，b∈R)，且f2(x)在(－∞，1]上单调递增，在[1，3]上单调递减．
(1)求a、b之间的关系式；
(2)当b＞3时，是否存在实数m，使得函数f(x)＝f12(x)
(x)－m2x在区间(0，＋∞)上为单调函数？若存在，请求出m的取值范围；若不存在，请说明理由．
已知f(x)是定义域为R的偶函数，且在区间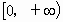
上是减函数，则
的单调递增区间是
[ ]
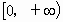
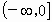
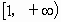
与[0，1]对于函数y＝f(x)(x∈D，D是此函数的定义域)若同时满足下列条件：
(Ⅰ)f(x)在D内单调递增或单调递减；
(Ⅱ)存在区间[a，b]
D，使f(x)在[a，b]上的值域为[a，b]；那么，把y＝f(x)(x∈D)叫闭函数．
(1)求闭函数y＝－x3符合条件(Ⅱ)的区间[a，b]；
(2)判断函数f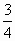(x)＝
x＋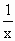
(x∈R+)是否为闭函数？并说明理由；
(3)若y＝k＋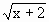
是闭函数，求实数k的取值范围．
设f(x)＝Asin(ωx＋φ)，
x1，x2∈R，使f(x1)－f(x2)取得最大值2时，|x1－x2|最小值为x，若f(x)在
上单调递增，在
上单调递减速，则
等于
A．－2
B．－1
C．0
D．1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com