
题目列表(包括答案和解析)
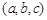 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果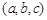 的极差
的极差 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 实施操作
实施操作 ,…,实施
,…,实施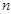 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
,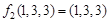 .
. ,求
,求 和
和 的值;
的值; 的极差为
的极差为 且
且 ,若
,若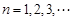 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值; 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在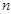 满足
满足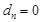 .
.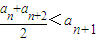 ; ②存在实数M,使得an≤M成立.
; ②存在实数M,使得an≤M成立. (n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;
(n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;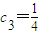 ,
,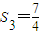 ,证明:数列{Sn}具有“性质m”,并指出M的取值范围;
,证明:数列{Sn}具有“性质m”,并指出M的取值范围; (n∈N*).对于任意的n≥3(n∈N*).
(n∈N*).对于任意的n≥3(n∈N*).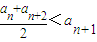 ;
; 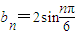 (n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;
(n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;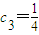 ,
,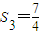 ,求证:数列{Sn}具有“性质m”;
,求证:数列{Sn}具有“性质m”;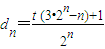 (n∈N*).对于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,求实数t的取值范围.
(n∈N*).对于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,求实数t的取值范围.设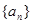 是公比为
是公比为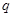 的等比数列,首项
的等比数列,首项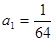 ,对于
,对于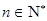 ,
,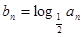 ,当且仅当
,当且仅当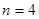 时,数列
时,数列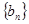 的前
的前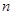 项和取得最大值,则
项和取得最大值,则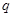 的取值范围为( )
的取值范围为( )
A.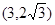 B.
B.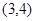 C.
C.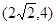 D.
D.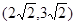
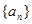 是公比为
是公比为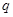 的等比数列,首项
的等比数列,首项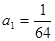 ,对于
,对于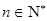 ,
,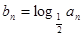 ,当且仅当
,当且仅当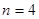 时,数列
时,数列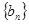 的前
的前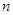 项和取得最大值,则
项和取得最大值,则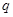 的取值范围为( )
的取值范围为( )A.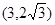 | B.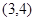 | C.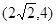 | D.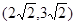 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com