
题目列表(包括答案和解析)
由于电脑故障,使得随机变量X的分布列中部分数据丢失(以“x,y”代替),其表如下:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 0.20 | 0.10 | 0.x5 | 0.10 | 0.1y | 0.20 |
则丢失的两个数据依次为 .
某城市出租汽车的起步价为10元,行驶路程不超出4km时租车费为10元,若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足lkm的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机经常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程X是一个随机变量.设他所收租车费为![]()
(1)求租车费![]() 关于行车路程X的关系式;
关于行车路程X的关系式;
(2)若随机变量X的分布列为
| X | 15 | 16 | 17 | 18 |
| P | 0.1 | 0.5 | 0.3 | 0.1 |
求所收租车费![]() 的数学期望.
的数学期望.
(3)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为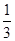 ,去参加乙游戏的概率为
,去参加乙游戏的概率为 .
.
设“这4个人中恰有i人去参加甲游戏”为事件

则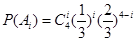 .
.
(1)这4个人中恰有2人去参加甲游戏的概率
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则 .由于
.由于 互斥,故
互斥,故
所以,这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为 .
.
(3) 的所有可能取值为0,2,4.由于
的所有可能取值为0,2,4.由于 互斥,
互斥, 互斥,故
互斥,故
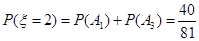

所以 的分布列是
的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量 的数学期望
的数学期望 .
.
| X | 15 | 16 | 17 | 18 |
| P | 0.1 | 0.5 | 0.3 | 0.1 |
| X | 15 | 16 | 17 | 18 |
| P | 0.1 | 0.5 | 0.3 | 0.1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com