
题目列表(包括答案和解析)
如图K53-3所示,体积相同的玻璃瓶甲、乙分别装满温度为60℃和0℃的热水和冷水
(1)关于温度,下列说法中正确的是( )
A.温度是分子平均动能的标志,所以甲瓶中水分子的平均动能比乙瓶中水分子的平均动能大
B.温度越高,布朗运动愈显著,所以甲瓶中水分子的布朗运动比乙瓶中![]() 水分子的布朗运动更显著
水分子的布朗运动更显著
C.甲瓶中水的内能与乙瓶中水的内能一样大
D.由于甲、乙两瓶水体积相等,所以甲、乙两瓶中水分子间的平![]() 均距离相等
均距离相等
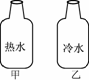
图K53-3
(2)已知水的分子量是18,若乙瓶中水的质量为3 kg,水的密度为1.0×103 kg/m3,阿伏加德罗常数NA=6.02×1023 mol-1,求乙瓶中水分子个数约为多少?(保留两位有效数字)
(10分)如图所示,质量分布不均匀的直细杆AB长1 m,将它的两端用两根细绳拴住吊在两竖直墙上,当AB在水平方向平衡时,细绳AC与竖直方向的夹角为θ1=60°,细绳BD与竖直方向的夹角为θ2=30°.求AB杆的重心距B端的距离.
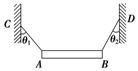
图4-18
【解析】:以AB杆为研究对象,受力分析如图所示,AC绳的拉力为F1,BD绳的拉力为F2.F1、F2的作用线交于E点,则重力G的作用线必过E点.过E点作竖直线交AB杆于O点,O点即为AB杆重心的位置.
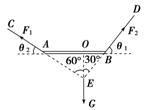 [来源:学§科§网]
[来源:学§科§网]
由几何关系可知
=·sin30°=·sin30°·sin30°
==0.25 m.
即细杆的重心距B端0.25 m.
(10分)如图所示,质量分布不均匀的直细杆AB长1 m,将它的两端用两根细绳拴住吊在两竖直墙上,当AB在水平方向平衡时,细绳AC与竖直方向的夹角为θ1=60°,细绳BD与竖直方向的夹角为θ2=30°.求AB杆的重心距B端的距离.
图4-18
【解析】:以AB杆为研究对象,受力分析如图所示,AC绳的拉力为F1,BD绳的拉力为F2.F1、F2的作用线交于E点,则重力G的作用线必过E点.过E点作竖直线交AB杆于O点,O点即为AB杆重心的位置.
由几何关系可知
=·sin30°=·sin30°·sin30°
==0.25 m.
即细杆的重心距B端0.25 m.
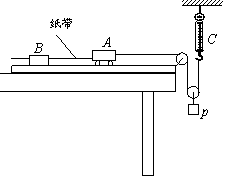
(8分)某同学用如图所示的实验装置探究小车动能变化与合外力对它所做功的关系。图中A为小车,连接在小车后面的纸带穿过打点计时器B的限位孔,它们均置于水平放置的一端带有定滑轮的足够长的木板上,C为弹簧测力计,不计绳与滑轮的摩擦。实验时,先接通电源再松开小车,打点计时器在纸带上打下一系列点。
(1)该同学在一条比较理想的纸带上,从点迹清楚的某点开始记为O点,顺次选取5个点,分别测量这5个点到O之间的距离,并计算出它们与O点之间的速度平方差△v2(△v2=v2-v02),填入下表:
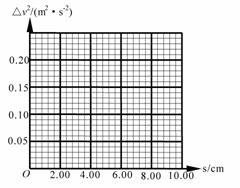
请以△v2为纵坐标,以s为横坐标在方格纸中作出△v2—s图象.若测出小车质量为0.2kg,结合图象可求得小车所受合外力的大小为_______N
(2)若该同学通过计算发现小车所受合外力小于测力计读数,明显超出实验误差的正常范围.你认为主要原因是__________________________________________________,实验操作中改进的措施是________________________________________________。
| 点迹 | s/cm | △v 2/m2·s-2 |
| O | / | / |
| 1 | 1.60 | 0.04 |
| 2 | 3.60 | 0.09 |
| 3 | 6.00 | 0.15 |
| 4 | 7.00 | 0.18 |
| 5 | 9.20 | 0.23 |
(10分)两个完全相同的物块A、B,质量均为m=0.8 kg,在同一粗糙水平面上以相同的初速度从同一位置开始运动。如图18中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象,求:
(1)物块A所受拉力F的大小;
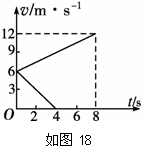 (2)8 s末物块A、B之间的距离x。
(2)8 s末物块A、B之间的距离x。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com