
题目列表(包括答案和解析)
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| L/cm | 0 | 36.0 | 49.0 | 64.0 | 81.0 | 100.0 | 121.0 |
| T/s | 0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 |
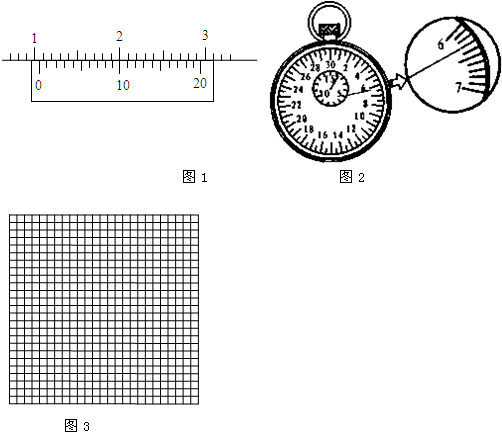
 (2013?浙江模拟)在“探究单摆的周期与摆长的关系”的实验中,小明现在已经准备了中心有孔的小钢球、不易伸长的细线、铁架台及铁夹和游标卡尺.
(2013?浙江模拟)在“探究单摆的周期与摆长的关系”的实验中,小明现在已经准备了中心有孔的小钢球、不易伸长的细线、铁架台及铁夹和游标卡尺. |
摆线长l/10-2m | 摆长L=l+d/2m-2 | 30次全振动的时间t/s | 周期T/s | T2/s2 |
|
… | ||||
| 1 | 31.50 | 32.135 | 30.7 | 1.02 | 1.04 | 1.01 | … | ||||
| 2 | 40.00 | 40.635 | 40.8 | 1.36 | 1.85 | 1.17 | … | ||||
| 3 | 50.00 | 50.635 | 44.5 | 1.48 | 2.19 | 1.22 | … | ||||
| 4 | 65.00 | 65.635 | 49.3 | 1.64 | 2.69 | 1.28 | … | ||||
| 5 | 79.00 | 79.635 | 53.8 | 1.79 | 3.20 | 1.34 | … | ||||
| 6 | 85.00 | 85.635 | 56.1 | 1.87 | 3.50 | 1.37 | … | ||||
| 7 | 97.50 | 98.135 | 60.1 | 2.00 | 4.00 | 1.41 | … |
Ⅰ(8分)某同学用实验的方法探究影响单摆周期的因素。
①他组装单摆是,在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,如图所示,这样做的目的是 (填字母代号)
A.保证摆动过程中摆长不变
B.可使周期测量得更加准确
C.需要改变摆长时便于调节
D.保证摆球在同一竖直平面内摆动
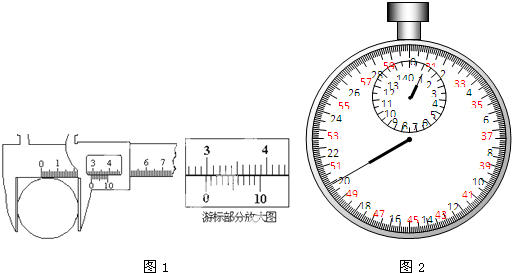
②他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径为12mm,单摆摆长为 m
③下列振动图像真实地描述了对摆长约为1m的单摆进行周期测量的四种操作过程,图中横坐标远点表示计时开始,A、B、C均为30次全振动的图像,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是 (填字母代号)

Ⅱ(10)在“测定金属的电阻率”实验中,所用测量仪器均已校准.待测金属丝接入电路部分的长度约为50cm.直径为0.396mm
(1)用伏安法测金属丝的电阻Rx.实验所用器材为:电池组(电动势为3V,内阻约1Ω)、电流表(内阻约0.1Ω)、电压表(内阻约3kΩ)、滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干. 某小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
|
次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
U/V |
0.10 |
0.30 |
0.70 |
1.00 |
1.50 |
1.70 |
2.30 |
|
I/A |
0.020 |
0.060 |
0.160 |
0.220 |
0.340 |
0.460 |
0.520 |
由以上数据可知,他们测量Rx是采用图2中的_________图(选填“甲”或“乙”).

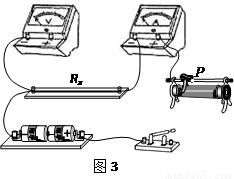
(2)图3是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的一端.请根据图(2)所选的电路图,补充完成图3中实物间的连线,并使闭合开关的瞬间,电压表或电流表不至于被烧坏.

(3)这个小组的同学在坐标纸上建立U、I坐标系,如图4所示,图中已标出了测量数据对应的4个坐标点.请在图4中标出第2、4、6次测量数据坐标点,并描绘出U─I图线.由图线得到金属丝的阻值Rx=___________Ω(保留两位有效数字).
(4)根据以上数据可以估算出金属丝的电阻率约为___________(填选项前的符号).
A.1×10-2Ω m B.1×10-3Ω
m B.1×10-3Ω m C.1×10-6Ω
m C.1×10-6Ω m D.1×10-8Ω
m D.1×10-8Ω m
m
(5)任何实验测量都存在误差.本实验所用测量仪器均已校准,下列关于误差的说法中正确的选项是___________(有多个正确选项).
A.用螺旋测微器测量金属丝直径时,由于读数引起的误差属于系统误差
B.由于电流表和电压表内阻引起的误差属于偶然误差
C.若将电流表和电压表内阻计算在内,可以消除由测量仪表引起的系统误差
D.用U─I图像处理数据求金属丝电阻可以减小偶然误差
A.研究平抛物体的运动 B.验证机械能守恒定律
C.验证动量守恒定律 D.用单摆测定重力加速度
(2)测量一螺线管两接线柱之间金属丝的长度。
器材:A.待测螺线管L(符号![]() ):绕制螺线管金属丝的电阻率ρ=5.0×10-7 Ω·m,电阻R1约为100 Ω
):绕制螺线管金属丝的电阻率ρ=5.0×10-7 Ω·m,电阻R1约为100 Ω
B.螺旋测微器
C.电流表G:量程100 μA,内阻Rg=500 Ω
D.电压表V:量程6 V,内阻RV=4 kΩ
E.定值电阻R0:R0=50 Ω
F.滑动变阻器R′:全电阻约1 kΩ
G.电源E:电动势9 V,内阻忽略不计
H.电键S一个,导线若干
①实验中用螺旋测微器测得金属丝的直径如图甲所示,其示数为d=_________________

图甲
②按图乙所示电路测量金属丝的电阻,请在图丙的实物图上连线。


图乙 图丙
③若测得的金属丝直径用d表示,电流表G的读数用I表示,电压表V的读数用U表示,则由已知量和测得量的符号表示金属丝的长度l=_________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com