
题目列表(包括答案和解析)
解不等式:(1) 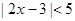 (2)
(2)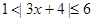
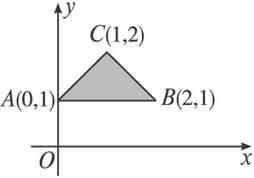
当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y
取得最大值的一个最优解为(1,2),则实数k的取值范围是( )

A.(-∞,-1]∪[1,+∞) B.[-1,1]
C.(-∞,-1)∪(1,+∞) D.(-1,1)
A.(-∞,-1]∪[1,+∞) B.[-1,1]
C.(-∞,-1)∪(1,+∞) D.(-1,1)
A.(1)只有一解,(2)也只有一解
B.(1)(2)都有两解
C.(1)有两解,(2)有一解
D.(1)只有一解,(2)有两解
解不等式
(1)![]()
(2)|x-1|+|2-x|>3+x
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com