
题目列表(包括答案和解析)
 如图所示,在水平地面上固定一倾角θ=37°的斜面体,物体A以某一初速度从斜面体底端沿斜面向上抛出,在物体A的正上方,有一物体B以某一初速度水平抛出.A、B均可看作质点,已知sin37°=0.6,cos37°=0.8,g取10m/s2.
如图所示,在水平地面上固定一倾角θ=37°的斜面体,物体A以某一初速度从斜面体底端沿斜面向上抛出,在物体A的正上方,有一物体B以某一初速度水平抛出.A、B均可看作质点,已知sin37°=0.6,cos37°=0.8,g取10m/s2. 如图所示是放置在竖直平面内的游戏滑轨,有一质量m=2kg的小球穿在轨道上.滑轨由四部分粗细均匀的滑杆组成;水平轨道AB;与水平面间的成夹角θ=370且长L=6m的倾斜直轨道CD;半径R=1m的圆弧轨道APC;半径R=3m的圆弧轨道BQED.直轨道与圆弧轨道相切,切点分别为A、B、D、C,E为最低点.倾斜轨道CD与小球间的动摩擦因数μ=
如图所示是放置在竖直平面内的游戏滑轨,有一质量m=2kg的小球穿在轨道上.滑轨由四部分粗细均匀的滑杆组成;水平轨道AB;与水平面间的成夹角θ=370且长L=6m的倾斜直轨道CD;半径R=1m的圆弧轨道APC;半径R=3m的圆弧轨道BQED.直轨道与圆弧轨道相切,切点分别为A、B、D、C,E为最低点.倾斜轨道CD与小球间的动摩擦因数μ=| 5 | 32 |
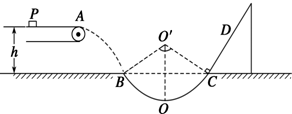 如图所示,水平传送带以5m/s的速度沿顺时针方向运动,在传送带上的P点轻轻地放上一质量m=1kg的小物块,PA间的距离为1.5m,小物块随传送带运动到A点后水平抛出,恰好沿圆弧切线从B点进入竖直光滑圆弧轨道运动.B、C为圆弧的两端点其连线水平,CD为与C点相切的一固定斜面.小物块离开C点后经0.8s通过D点.已知小物块与传送带间的动摩擦因数μ1=0.3,圆弧轨道最低点为O,A点与水平面的高度差h=0.8m,小物块与斜面间的动摩擦因数μ2=
如图所示,水平传送带以5m/s的速度沿顺时针方向运动,在传送带上的P点轻轻地放上一质量m=1kg的小物块,PA间的距离为1.5m,小物块随传送带运动到A点后水平抛出,恰好沿圆弧切线从B点进入竖直光滑圆弧轨道运动.B、C为圆弧的两端点其连线水平,CD为与C点相切的一固定斜面.小物块离开C点后经0.8s通过D点.已知小物块与传送带间的动摩擦因数μ1=0.3,圆弧轨道最低点为O,A点与水平面的高度差h=0.8m,小物块与斜面间的动摩擦因数μ2=| 1 | 3 |
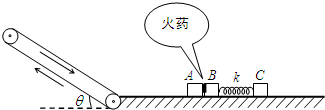 如图所示,倾角θ=37°的粗糙传送带与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,传送带始终以v=3m/s的速率顺时针匀速转动,A、B、C滑块的质量为 mA=1kg,mB=2kg,mC=3kg,(各滑块均视为质点).A、B间夹着质量可忽略的火药.k为处于原长的轻质弹簧,两端分别与B和C连接.现点燃火药(此时间极短且不会影响各物体的质量和各表面的光滑程度),滑块A以6m/s水平向左冲出,接着沿传送带向上前进,已知滑块A与传送带间的动摩擦因数为μ=0.75,传送带与水平面足够长,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,倾角θ=37°的粗糙传送带与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,传送带始终以v=3m/s的速率顺时针匀速转动,A、B、C滑块的质量为 mA=1kg,mB=2kg,mC=3kg,(各滑块均视为质点).A、B间夹着质量可忽略的火药.k为处于原长的轻质弹簧,两端分别与B和C连接.现点燃火药(此时间极短且不会影响各物体的质量和各表面的光滑程度),滑块A以6m/s水平向左冲出,接着沿传送带向上前进,已知滑块A与传送带间的动摩擦因数为μ=0.75,传送带与水平面足够长,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: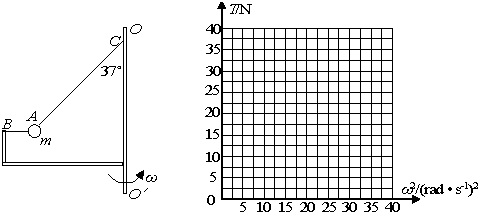
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com