
题目列表(包括答案和解析)
某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,图4-2-13甲为实验装置简图(交流电的频率为50 Hz).

图4-2-13
(1)图乙为某次实验得到的纸带,根据纸带可求出小车的加速度大小为________m/s2(保留两位有效数字).
(2)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的![]() ,数据如下表:
,数据如下表:
| 实验次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/(m·s-2) | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
|
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在如图4-2-14所示的方格坐标纸中画出a-![]() 图线,并依据图线求出小车加速度a与质量倒数
图线,并依据图线求出小车加速度a与质量倒数![]() 之间的关系式是________.
之间的关系式是________.

图4-2-14

图4-2-15
(3)保持小车质量不变,改变砂和砂桶质量,该同学根据实验数据作出了加速度a随合力F的变化图线,如图4-2-15所示.该图线不通过原点,请你分析其主要原因是________________________________________________________________________
________________________________________________________________________.
某实验小组设计如图甲所示电路探究硅光电池,给硅光电池加反向电压(硅光电池负极接高电势点,正极接低电势点),探究其在无光照时的反向伏安特性.图中电压表V1量程选用3 V,内阻为6.0 kΩ;电压表V2量程选用15 V,内阻约为30 kΩ;R0为保护电阻;直流电源电动势E约为12 V,内阻不计.(硅光电池在无光照时不产生电能,可视为一电子元件)
①根据图甲,用笔画线代替导线,将图乙连接成完整电路.
②用遮光罩罩住硅光电池,闭合开关S,调节变阻器R,读出电压表V1、V2的示数U1、U2.
(ⅰ)某次测量时,电压表V1示数如图丙,则U1= V,可算出通过硅光电池的反向电流大小为________mA(保留两位小数).
(ⅱ)该小组测出大量数据,筛选出下表所示的9组U1、U2数据,算出相应的硅光电池两端反向电压Ux和通过的反向电流Ix(表中“-”表示反向),并在坐标纸上建立Ix-Ux坐标系,标出了与表中前5组Ux、Ix数据对应的5个坐标点.请你标出余下的4个坐标点,并绘出Ix-Ux图线.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
U1/V | 0.00 | 0.00 | 0.06 | 0.12 | 0.24 | 0.42 | 0.72 | 1.14 | 1.74 |
U2/V | 0.0 | 1.0 | 2.1 | 3.1 | 4.2 | 5.4 | 6.7 | 8.1 | 9.7 |
Ux/V | 0.0 | -1.0 | -2.0 | -3.0 | -4.0 | -5.0 | -6.0 | -7.0 | -8.0 |
Ix/mA | 0.00 | 0.00 | -0.01 | -0.02 | -0.04 | -0.07 | -0.12 | -0.19 | -0.29 |
(ⅲ)由Ix-Ux图线可知,硅光电池无光照下加反向电压时,Ix与Ux成 (填“线性”或“非线性”)关系.




如图,传送带与水平面倾角θ=37°,以10米/秒的速率逆时针转动,在传送带上端A处轻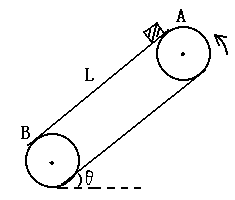 轻放一质量m=2千克的物块,它与传送带间的摩擦系数μ=0.5。若两轮间传送带的长度L=29米。(g取10米/秒2, sin37°=0.6,cos37°=0.8)求:(1)物块从传送带上端A运动到 B处所用时间和到B处时的速度大小。(2)物块从传送带上端A运动到 B处的过程中摩擦力对物块所做的功。(3) 物块从传送带上端A运动到 B处的过程中物块和传送带所产生的总热量。
轻放一质量m=2千克的物块,它与传送带间的摩擦系数μ=0.5。若两轮间传送带的长度L=29米。(g取10米/秒2, sin37°=0.6,cos37°=0.8)求:(1)物块从传送带上端A运动到 B处所用时间和到B处时的速度大小。(2)物块从传送带上端A运动到 B处的过程中摩擦力对物块所做的功。(3) 物块从传送带上端A运动到 B处的过程中物块和传送带所产生的总热量。
某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,图S4-7甲为实验装置简图.(交流电的频率为50 Hz)

甲 乙
图S4-7
(1)如图乙所示为某次实验得到的纸带,根据纸带可求出小车的加速度大小为__________m/s2.(保留两位有效数字)
(2)保持沙和沙桶质量不变,改变小车质量 m,分别得到小车加速度a与质量 m及对应的![]() 数据如下表:
数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度 a/m·s-2 | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质 量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
|
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在如图S4-8所示的坐标纸中画出a-![]() 图线,并由图线求出小车加速度a与质量倒数
图线,并由图线求出小车加速度a与质量倒数![]() 之间的关系式是________________.
之间的关系式是________________.
 图S4-8
图S4-8
某同学设计了一个“探究加速度与物体所受合力F及质量m的关系”实验.如图a为实验装置简图,A为小车,B为电火花计时器,C为装有砝码的小桶,D为一端带有定滑轮的长方形木板,实验中认为细绳对小车拉力F等于砝码和小桶的总重量,小车运动加速度a可用纸带上的打点求得.
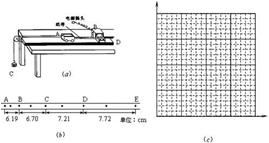
(1)图(b)为某次实验得到的纸带,根据纸带可求出小车的加速度大小为 m/s2.(保留二位有效数字)
(2)在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如下表:
|
次 数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
小车加速度a/m?s-2 |
1.98 |
1.72 |
1.48 |
1.25 |
1.00 |
0.75 |
0.48 |
0.50 |
0.30 |
|
小车质量m/kg |
0.25 |
0.29 |
0.33 |
0.40 |
0.50 |
0.71 |
0.75 |
1.00 |
1.67 |
|
|
|
|
|
|
|
|
|
|
|
根据上表数据,为直观反映F不变时a与m的关系,请在图c 方格坐标纸中选择恰当物理量建立坐标系,并作出图线.(如有需要,可利用上表中空格)
(3)在“探究加速度与力的关系”时,保持小车的质量不变,改变小桶中砝码的质量,该同学根据实验数据作出了加速度a与合力F图线如图d,该图线不通过坐标原点,试分析图线不通过坐标原点的原因.答: 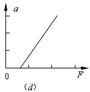
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com