
题目列表(包括答案和解析)
两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星’.现测得两星中心距离为R,运动周期为T,求:双星的总质量。
两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星’.现测得两星中心距离为R,运动周期为T,求:双星的总质量。
两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星’.现测得两星中心距离为R,运动周期为T,求:双星的总质量。
两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星”.现测得两星中心距离为R,运动周期为T,求:双星的总质量。
解:设双星的质量分别为M1、M2。它们绕其连线上的O点以周期T作匀速圆周运动,由万有引力定律及牛顿第二定律得:
![]()
联立解得: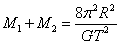
上述结果是否正确?若正确,请列式证明:若错误,请求出正确结果。
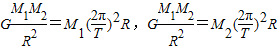 联立解得:
联立解得: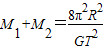
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com