
题目列表(包括答案和解析)
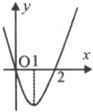 5、已知在R上的可导函数f(x)的图象如图所示,则不等式(x-2)f(x)>0的解集为( )
5、已知在R上的可导函数f(x)的图象如图所示,则不等式(x-2)f(x)>0的解集为( )A.![]() B.
B.![]()
C.![]() 或
或![]() D.不同于A、B、C的其他答案
D.不同于A、B、C的其他答案
回忆你所学过的函数分别写出符合下列条件的一个函数式.
(1)f(x)+f(y)=f(x+y) 答:
(2)f(x)f(y)=f(x+y) 答:
(3)f(x)+f(y)=f(xy) 答:
(4)f(x)f(y)=f(xy) 答:
(要求:以上四个答案为四种不同类型的函数.如:函数f(x)=x+1与函数f(x)=2x+3属于同类型的函数)
①当b<0,解集为R ②当b=0时,解集为{a}?③当b>0时,解集为{x|x<a-b或x>a+b}
A.①② B.②③ C.①③ D.①②③
设qÎ(0,2p),且q ¹p,z1=1+cosq +isinq ,z2=1-cosq +isinq ,则argz1+argz2的值为( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.不同于A、B、C的其他答案
D.不同于A、B、C的其他答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com