
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,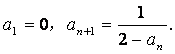
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
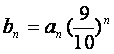 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有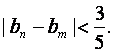
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
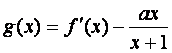 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
一、选择题1―5 BDADA 6―12 ACDCB BB
二、填空题13.2 14. 15.
15. 16.①③④
16.①③④
三、17.解:在 中
中 

 2分
2分

 4分
4分



 ….6分
….6分
(2) =
= ……..10分
……..10分
18.解:(1)在正方体 中,
中, 、
、 、
、 、
、 分别为
分别为 、
、 、
、 、
、 中点
中点 
 即
即 平面
平面

 到平面
到平面 的距离即
的距离即 到平面
到平面 的距离.
的距离.
在平面 中,连结
中,连结 则
则
故 到
到 之距为
之距为 , 因此
, 因此 到平面
到平面 的距离为
的距离为 ………6分
………6分
(2)在四面体 中,
中,
又底面三角形 是正三角形,
是正三角形,
 :
:
设 到
到 之距为
之距为



故 与平面
与平面 所成角
所成角 的正弦值
的正弦值  …………12分
…………12分
19.解:(Ⅰ)设 、
、 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为 、
、
由题意得: ……………………2分
……………………2分
解得: 或
或 ,∴
,∴ . 即,一个零件经过检测为合格品的概率为
. 即,一个零件经过检测为合格品的概率为 ………………………………..
3分
………………………………..
3分
(Ⅱ)任意抽出5个零件进行检查,其中至多3个零件是合格品的概率为
 ……………………………….8分
……………………………….8分
(Ⅲ)依题意知 ~B(4,
~B(4, ),
), ,
, …………12分
…………12分
20.解(1)



 。…………………………………………………2分
。…………………………………………………2分

 …………………………………………………………….4分
…………………………………………………………….4分

 为等差数列
为等差数列  6分
6分
(2)
 ………………10分
………………10分
21.解:(1)

 2分
2分
x
(- ,-3)
,-3)
-3
(-3,1)
1
(1,+ )
)

+
0
-
0
+
 (x)
(x)
增
极大值
减
极小值
增

 6分
6分
(2)







 9分
9分
 3
3 恒成立
恒成立
 3
3 恒成立
恒成立

 恒成立…………………………..10分
恒成立…………………………..10分





 12分
12分
22.解法一:(Ⅰ)设点 ,则
,则 ,由
,由 得:
得:
 ,化简得
,化简得 .……………….3分
.……………….3分
(Ⅱ)(1)设直线 的方程为:
的方程为:
 .
.
设 ,
, ,又
,又 ,
,
联立方程组 ,消去
,消去 得:
得: ,
, ,
,
 ……………………………………6分
……………………………………6分
 由
由 ,
, 得:
得:
 ,
, ,整理得:
,整理得:
 ,
, ,
,



 .……………………………………………………………9分
.……………………………………………………………9分
解法二:(Ⅰ)由 得:
得: ,
,
 ,
,
 ,
, .
.
所以点 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.
(Ⅱ)(1)由已知 ,
, ,得
,得 .
.
则: .…………①
.…………①
过点 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,
则有: .…………②
.…………②
 ,
, .
.
所以点 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.
(Ⅱ)(1)由已知 ,
, ,得
,得 .
.
则: .…………①
.…………①
过点 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,
则有: .…………②
.…………②
由①②得: ,即
,即 .
.
(Ⅱ)(2)解:由解法一,



 .
.
当且仅当 ,即
,即 时等号成立,所以
时等号成立,所以 最小值为
最小值为 .…………..12分
.…………..12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com