21. 已知函数其中a<0,且a≠-1. (Ⅰ)讨论函数的单调性, (Ⅱ)设函数.是否存在a.使在[a,-a]上为减函数?若存在.求a的取值范围,若不存在.请说明理由. 已知是给定的实常数.设函数.. 是的一个极大值点. (Ⅰ)求的取值范围, (Ⅱ)设是的3个极值点.问是否存在实数.可找到.使得的某种排列(其中=)依次成等差数列?若存在.求所有的及相应的,若不存在.说明理由. 解析:本题主要考查函数极值的概念.导数运算法则.导数应用及等差数列等基础知识.同时考查推理论证能力.分类讨论等综合解题能力和创新意识. =ex(x-a) 令 于是.假设 (1) 当x1=a 或x2=a时.则x=a不是f(x)的极值点.此时不合题意. (2) 当x1a且x2a时.由于x=a是f(x)的极大值点.故x1<a<x2. 即 即 所以b<-a 所以b的取值范围是 此时 或 (2)当时.则或 于是 此时 综上所述.存在b满足题意. 当b=-a-3时. 时. 时. 设函数. (Ⅰ)证明:当时., (Ⅱ)设当时..求a的取值范围. [命题意图]本题主要考查导数的应用和利用导数证明不等式.考查考生综合运用知识的能力及分类讨论的思想.考查考生的计算能力及分析问题.解决问题的能力. 【
查看更多】
题目列表(包括答案和解析)
(2010湖南文数)2. 下列命题中的假命题是
A. 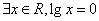 B.
B. 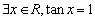
C. 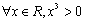 D.
D. 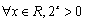
查看答案和解析>>
(2010湖南文数)2. 下列命题中的假命题是
A. 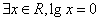 B.
B. 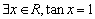
C. 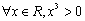 D.
D. 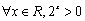
查看答案和解析>>

![]() B.
B. ![]()
![]() D.
D. ![]()
![]() B.
B. ![]()
![]() D.
D. ![]()