
题目列表(包括答案和解析)
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
|
| β |
|
| α |
| α |
| β |
|
| π |
| 4 |
(本题满分12分) 已知mod(a,b)是一个函数,它的意义指的是整数 除以整数
除以整数 所得的余数。下面请你阅读下列在Scilab环境下编写的程序:
所得的余数。下面请你阅读下列在Scilab环境下编写的程序:
S=0;
for i=1:1:100
if mod(i,2)==1
S=S+i^2;
else
S=S-i^2;
end;
end;
print(%io(2),S)
回答下列问题:(1)此程序中包括了哪些基本算法语句?
(2)画出此算法对应的程序框图;
(3)在Scilab环境下用while语句重新设计此程序。
(本题满分12分)
如图,斜率为1的直线 过抛物线
过抛物线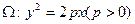 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线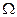 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求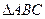 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线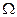 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)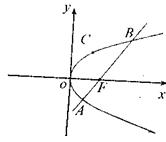
(本题满分12分)
如图,斜率为1的直线![]() 过抛物线
过抛物线![]() 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线![]() 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求![]() 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线![]() 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com