
题目列表(包括答案和解析)
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对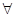 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对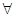 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe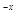 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
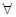 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;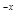 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.(本小题满分14分)
已知点P ( t , y )在函数f ( x ) = ![]() (x ?? –1)的图象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(x ?? –1)的图象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(1) 求证:| ac | ?? 4;(2) 求证:在(–1,+∞)上f ( x )单调递增.(3) (仅理科做)求证:f ( | a | ) + f ( | c | ) > 1.
.(本题满分14分)已知函数f(x)=sin(ωx+φ),其中ω>0,|φ|< .
.
(1)若cos cosφ-sin
cosφ-sin sinφ=0,求φ的值;
sinφ=0,求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于 ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com