
题目列表(包括答案和解析)
用数学归纳法证明:
 .
.
【解析】首先证明当n=1时等式成立,再假设n=k时等式成立,得到等式
 ,
,
下面证明当n=k+1时等式左边
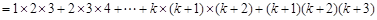 ,
,
根据前面的假设化简即可得到结果,最后得到结论.
试判断下面的证明过程是否正确:
用数学归纳法证明:
![]()
证明:(1)当![]() 时,左边=1,右边=1
时,左边=1,右边=1
∴当![]() 时命题成立.
时命题成立.
(2)假设当![]() 时命题成立,即
时命题成立,即
![]()
则当![]() 时,需证
时,需证
![]()
由于左端等式是一个以1为首项,公差为3,项数为![]() 的等差数列的前
的等差数列的前![]() 项和,其和为
项和,其和为
![]()
∴![]() 式成立,即
式成立,即![]() 时,命题成立.根据(1)(2)可知,对一切
时,命题成立.根据(1)(2)可知,对一切![]() ,命题成立.
,命题成立.
试判断下面的证明过程是否正确:
用数学归纳法证明:
![]()
证明:(1)当![]() 时,左边=1,右边=1
时,左边=1,右边=1
∴当![]() 时命题成立.
时命题成立.
(2)假设当![]() 时命题成立,即
时命题成立,即
![]()
则当![]() 时,需证
时,需证
![]()
由于左端等式是一个以1为首项,公差为3,项数为![]() 的等差数列的前
的等差数列的前![]() 项和,其和为
项和,其和为
![]()
∴![]() 式成立,即
式成立,即![]() 时,命题成立.根据(1)(2)可知,对一切
时,命题成立.根据(1)(2)可知,对一切![]() ,命题成立.
,命题成立.
试判断下面的证明过程是否正确:
用数学归纳法证明:
1+4+7+…3n-2)=![]() (3n-1)
(3n-1)
(15分)观察下面等式,归纳出一般结论,并用数学归纳法证明你的结论。
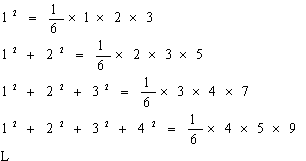
结论:![]() :
:
ww w.k s5 u.co m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com