
题目列表(包括答案和解析)
(本小题满分15分)
已知函数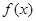 的图象在
的图象在 上连续不断,定义:
上连续不断,定义:  ,
,
其中,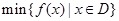 表示函数
表示函数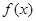 在
在 上的最小值,
上的最小值,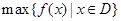 表示函数
表示函数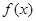 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得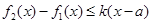 对任意的
对任意的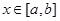 成立,则称函数
成立,则称函数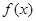 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若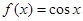 ,
,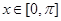 ,试写出
,试写出 的表达式;
的表达式;
(2)已知函数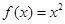 ,
,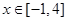 ,试判断
,试判断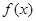 是否为
是否为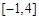 上的“
上的“ 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知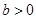 ,函数
,函数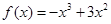 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求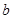 的取值范围.
的取值范围.
(本小题满分15分)
已知函数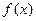 的图象在
的图象在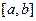 上连续不断,定义:
上连续不断,定义: 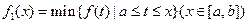 ,
,
其中, 表示函数
表示函数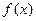 在
在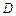 上的最小值,
上的最小值,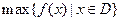 表示函数
表示函数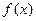 在
在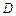 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数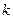 ,使得
,使得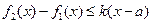 对任意的
对任意的 成立,则称函数
成立,则称函数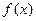 为
为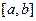 上的“
上的“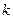 阶收缩函数”.
阶收缩函数”.
(1)若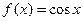 ,
,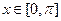 ,试写出
,试写出 的表达式;
的表达式;
(2)已知函数 ,
,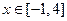 ,试判断
,试判断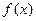 是否为
是否为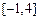 上的“
上的“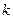 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的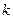 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知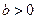 ,函数
,函数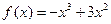 是
是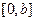 上的2阶收缩函数,求
上的2阶收缩函数,求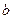 的取值范围.
的取值范围.
(本小题满分15分)已知函数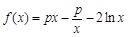 .
.
(I) 若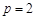 ,求曲线
,求曲线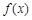 在点
在点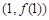 处的切线方程;
处的切线方程;
若函数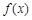 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数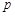 的取值范围;
的取值范围;
(III)设函数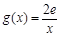 ,若在
,若在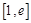 上至少存在一点
上至少存在一点 ,使得
,使得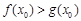 成立,求实数
成立,求实数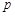 的取值范围.
的取值范围.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
A
C
D
D
C
B
A
B
二、填空题
11.  ;
12.
;
12.  (或
(或 ); 13. 15;
14. 6;
); 13. 15;
14. 6;
15.  16.
16.  ;
17.
;
17. 
 三、解答题
三、解答题

 …………12′
…………12′
 故函数
故函数 的取值范围是
的取值范围是 …………12′
…………12′
19. 解:(1)设袋中原有n个白球,由题意知: ,所以
,所以 =12,
=12,
解得n=4(舍去 ),即袋中原有4个白球;
…………4′
),即袋中原有4个白球;
…………4′
(2)由题意, 的可能取值为1,2,3,4
的可能取值为1,2,3,4

 所以,取球次数
所以,取球次数 的分布列为:
的分布列为:

1
2
3
4
P





 …………9′
…………9′
 (Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A,
(Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A,
 则
则 或 “
或 “ =
= …………14′
…………14′
20. 解:⑴由条件得: ∴
∴ ∵
∵ ∴
∴ ∴
∴ 为等比数列∴
为等比数列∴ …………4′
…………4′
⑵由 得
得 
又 ∴
∴  …………9′
⑶∵
…………9′
⑶∵

(或由 即
即 ),∴
),∴ 为递增数列.
为递增数列.
∴ 从而
从而
∴
 …………14′
…………14′
21.解:(1)依题意有 ,由显然
,由显然 ,得
,得 ,化简得
,化简得 ;
…………5′
;
…………5′
(2)证明:(?)



 …………10′
…………10′
(?)设点A、B的坐标分别为 ,不妨设点A在点P与点B之间,点
,不妨设点A在点P与点B之间,点 ,依(?)有
,依(?)有 *,又可设过点P(2,4)的直线方程为
*,又可设过点P(2,4)的直线方程为 ,得
,得 ,
,
 ,代入上*式得
,代入上*式得
 ,又
,又 ,得
,得
 ,当直线AB的斜率不存在时,也满足上式.即点Q总过直线
,当直线AB的斜率不存在时,也满足上式.即点Q总过直线 ,得证.
…………15′
,得证.
…………15′
22. 解:(Ⅰ)设 与
与 在公共点
在公共点 处的切线相同.
处的切线相同. ,
, ,由题意
,由题意 ,
, .即
.即 由
由 得:
得: ,或
,或 (舍去).即有
(舍去).即有 .
…………4′
.
…………4′
令 ,则
,则 .于是当
.于是当 ,即
,即 时,
时, ;
;
当 ,即
,即 时,
时, .故
.故 在
在 为增函数,在
为增函数,在 为减函数,于是
为减函数,于是 在
在 的最大值为
的最大值为 .
…………8′
.
…………8′
(Ⅱ)设
则
 .故
.故 在
在 为减函数,在
为减函数,在 为增函数,于是函数
为增函数,于是函数 在
在 上的最小值是
上的最小值是 .故当
.故当 时,有
时,有 ,即当
,即当 时,
时, .
…………15′
.
…………15′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com