
题目列表(包括答案和解析)
| l |
| 2 |
| l |
| 2 |
| r |
| 2 |

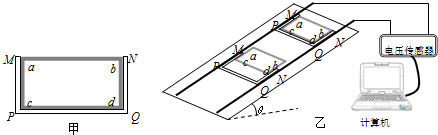
 如图甲所示,在竖直平面内有一水平向右的匀强电场,场强E=1.0×104N/C.电场内有一半径为R=2.0m的光滑绝缘细圆环形轨道竖直放置且固定,有一质量为m=0.4kg、带电荷量为q=+3.0×10-4C的带孔小球穿过细圆环轨道静止在位置A,现对小球沿切线方向作用一瞬时速度vA,使小球恰好能在光滑绝缘细圆环形轨道上做圆周运动,取圆环的最低点为重力势能和电势能的零势能点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图甲所示,在竖直平面内有一水平向右的匀强电场,场强E=1.0×104N/C.电场内有一半径为R=2.0m的光滑绝缘细圆环形轨道竖直放置且固定,有一质量为m=0.4kg、带电荷量为q=+3.0×10-4C的带孔小球穿过细圆环轨道静止在位置A,现对小球沿切线方向作用一瞬时速度vA,使小球恰好能在光滑绝缘细圆环形轨道上做圆周运动,取圆环的最低点为重力势能和电势能的零势能点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,求:
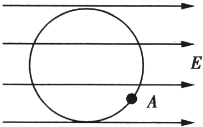
如图甲所示,CDE是固定在绝缘水平面上的光滑金属导轨,CD=DE=L,∠CDE=60°,CD和DE单位长度的电阻均为r0,导轨处于磁感应强度为B、竖直向下的匀强磁场中。 MN是绝缘水平面上的一根金属杆,其长度大于L,电阻可忽略不计。现MN在向右的水平拉力作用下以速度v0。在CDE上匀速滑行。MN在滑行的过程中始终与CDE接触良好,并且与C、E所确定的直线平行。
(1)求MN滑行到C、E两点时,C、D两点电势差的大小;
(2)推导MN在CDE上滑动过程中,回路中的感应电动势E与时间t的关系表达式;
(3)在运动学中我们学过:通过物体运动速度和时间的关系图线(v – t 图)可以求出物体运动的位移x,如图乙中物体在0 – t0。时间内的位移在数值上等于梯形Ov0Pt的面积。通过类比我们可以知道:如果画出力与位移的关系图线(F—x图)也可以通过图线求出力对物体所做的功。
请你推导MN在CDE上滑动过程中,MN所受安培力F安与MN的位移x的关系表达式,并用F安与x的关系图线求出MN在CDE上整个滑行的过程中,MN和CDE构成的回路所产生的焦耳热。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com