
题目列表(包括答案和解析)
(11·贵港)(本题满分11分,第(1)题5分,第(2)题6分)
(1)(11·贵港)(本题满分5分)计算:(-1)2011+ -2sin60º+|-1|;
-2sin60º+|-1|;

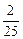 ,得到黄球的概率为
,得到黄球的概率为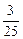 ,得到绿球的概率为
,得到绿球的概率为 .已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
.已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?(本题满分11分)某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)

1.(1)直接写出c的值;
2.(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
3.(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右测上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
(11·贵港)(本题满分11分)
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
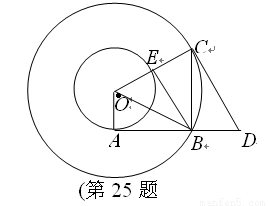
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
① 求y与x之间的函数关系式;
② 当BE与小圆相切时,求x的值.
(本题满分11分)
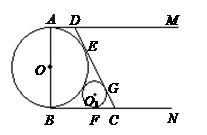
如图所示,⊙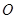 的直径
的直径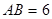 ,
,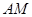 和
和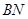 是它的两条切线,
是它的两条切线,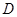 为射线
为射线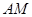 上的动点(不与
上的动点(不与 重合),
重合),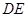 切⊙
切⊙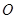 于
于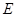 ,交
,交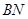 于
于 ,设
,设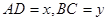 .
.
(1)求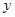 与
与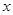 的函数关系式;
的函数关系式;
(2)若⊙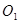 与⊙
与⊙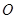 外切,且⊙
外切,且⊙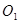 分别与
分别与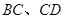
相切于点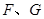 ,求
,求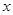 为何值时⊙
为何值时⊙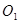 半径为1.
半径为1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com