题目列表(包括答案和解析)
设
是定义在区间
上的函数，其导函数为
。如果存在实数
和函数
，其中对任意的
都有>0，使得
，则称函数具有性质
。
(1)设函数
，其中
为实数。
(i)求证：函数具有性质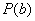
； (ii)求函数的单调区间。
(2)已知函数
具有性质
。给定
设
为实数，
，
，且
，
若|
|<|
|，求的取值范围。
数学Ⅱ（附加题）
设
是定义在区间
上的函数，其导函数为
。如果存在实数
和函数
，其中对任意的
都有>0，使得
，则称函数具有性质
。
(1)设函数
，其中
为实数。
(i)求证：函数具有性质
； (ii)求函数的单调区间。
(2)已知函数
具有性质
。给定
设
为实数，
，
，且
，
若|
|<|
|，求的取值范围。
（本小题满分16分）
设
是定义在区间
上的函数，其导函数为
。如果存在实数
和函数
，其中对任意的
都有>0，使得
，则称函数具有性质
。
(1)设函数
，其中
为实数。
(i)求证：函数具有性质
； (ii)求函数的单调区间。
(2)已知函数
具有性质
。给定
设
为实数，
，
，且
，
若|
|<|
|，求的取值范围。
设f(x)使定义在区间(1，＋∞)上的函数，其导函数为
．如果存在实数a和函数h(x)，其中h(x)对任意的x∈(1，＋∞)都有h(x)＞0，使得
(x)＝h(x)(x2－ax＋1)，则称函数f(x)具有性质P(a)．
(1)设函数f(x)＝h(x)＋
(x＞1)，其中b为实数
①求证：函数f(x)具有性质P(b)
②求函数f(x)的单调区间
(2)已知函数g(x)具有性质P(2)，给定x1，x2∈(1，＋∞)，x1＜x2，设m为实数，α＝mx1＋(1－m)x2，β＝(1－m)x1＋mx2，且α＞1，β＞1，若|g(α)－g(β)|＜|g(x1)－g(x2)|，求m的取值范围
定义函数
其导函数记为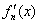
.
（1） 求证：
；
（2） 设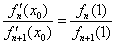
，求证：
；
（3） 是否存在区间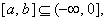
使函数
在区间
上的值域为
？
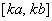若存在，求出最小的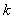
值及相应的区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com