
题目列表(包括答案和解析)
| A、t1>t0 t2<t1 | B、t1<t0 t2>t1 | C、t1>t0 t2>t1 | D、t1<t0 t2<t1 |
图
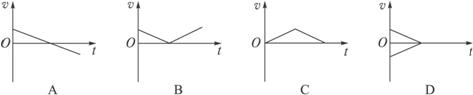
将一物体以某一初速度竖直上抛,如图所示的四幅图中,哪一幅能正确表示物体在整 个运动过程中的速率![]() 与时间
与时间![]() 的关系(不计空气阻力)? ( )
的关系(不计空气阻力)? ( )
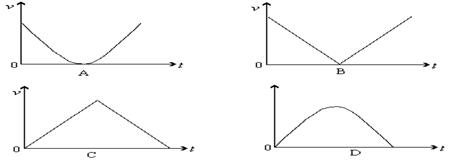
将一物体以某一初速度竖直上抛,图中哪幅能正确表示物体在整个运动过程中的速度大小v与时间t的关系(不计空气阻力)?( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com