
题目列表(包括答案和解析)
四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质,只要善于观察、乐于探索,我们会发现更多的结论.问题的提出:四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个小三角形,其中相对的两对三角形的面积之积有何关系?你能探索出结论吗?
(1)为了更直观的发现问题,我们不妨先在特殊的四边形——平行四边形中,研究这个问题:已知:在□ABCD中,O是对角线BD上任意一点(如图①)求证:S△OBC·S△OAD=S△OAB·S△OCD.

(2)有了(1)中的探索过程作参照,你一定能类比出一般四边形(如图②)中,解决问题的办法了吧!填写结论并写出证明过程.
已知:在四边形ABCD中,O是对角线BD上任意一点.(如图②)
求证:________.
证明:
(3)在三角形中(如图③),你能否归纳出类似的结论?若能,用文字叙述你归纳出的结论,并写出已知、求证和证明过程;若不能,说明理由.
 如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.
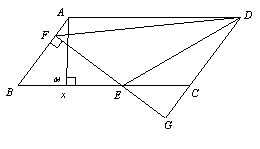
如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为 BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F. FE与DC的延长线相交于点G,连结DE,DF..
(1) 求证:ΔBEF ∽ΔCEG.
(2) 当点E在线段BC上运动时,△BEF和△CEG的周长之间有什么关系?并说明你的理由.
(3)设BE=x,△DEF的面积为 y,请你求出y和x之间的函数关系式,并求出当x为何值时,y有最大值,最大值是多少?
【解】

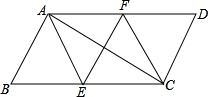 如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.
如图,平行四边形ABCD中,AE、CF分别是∠BAD和∠BCD的角平分线,根据现有的图形,请你添加一个条件,使四边形AECF为菱形,并说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com