
题目列表(包括答案和解析)
(本题满分18分)第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分。
圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦。已知椭圆C:![]() 。
。
 (1)过椭圆C的右焦点作一条垂直于
(1)过椭圆C的右焦点作一条垂直于![]() 轴的垂轴弦
轴的垂轴弦![]() ,求
,求![]() 的长度;
的长度;
(2)若点![]() 是椭圆C上不与顶点重合的任意一点,
是椭圆C上不与顶点重合的任意一点,![]() 是椭圆C的短轴,直线
是椭圆C的短轴,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() (如右图),求
(如右图),求![]() 的值;
的值;
(3)在(2)的基础上,把上述椭圆C一般化为![]() ,
,![]() 是任意一条垂直于
是任意一条垂直于![]() 轴的垂轴弦,其它条件不变,试探究
轴的垂轴弦,其它条件不变,试探究![]() 是否为定值?(不需要证明);请你给出双曲线
是否为定值?(不需要证明);请你给出双曲线![]() 中相类似的结论,并证明你的结论。
中相类似的结论,并证明你的结论。
(本题满分18分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
(Ⅲ)过A、B分别作抛物C的切线 且
且 交于点M,求
交于点M,求 与
与 面积之和的最小值.
面积之和的最小值.

(本小题满分12分)
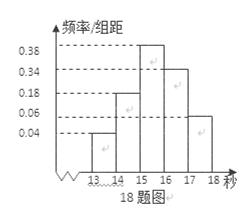
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组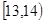 ,第二组
,第二组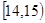 ……第五组
……第五组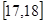 ,如图是按上述分组方法得到的频率分布直方图,根据有关规定,成绩小于16秒为达标.
,如图是按上述分组方法得到的频率分布直方图,根据有关规定,成绩小于16秒为达标.
(Ⅰ)用样本估计总体,某班有学生45人,设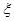 为达标人数,求
为达标人数,求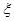 的数学期望与方差;
的数学期望与方差;
(Ⅱ)如果男女生使用相同的达标标准,则男女生达标情况如右表:
根据表中所给的数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: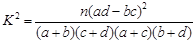
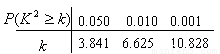
|
性别 是否 达标 |
男 |
女 |
合计 |
|
达标 |
|
|
_____ |
|
不达标 |
|
|
_____ |
|
合计 |
______ |
______ |
|
某单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中提取10人,然后再从这10人中选4人,那么至少有1人是“运动健将”的概率是多少?
(2)若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.

(本小题满分12分)
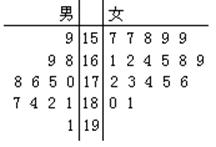
第4届湘台经贸洽谈交流会于2011年6月在我市举行 ,为了搞好接待工作,大会组委会在
某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎
叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”, 身高在175cm
以下(不包括175cm)定义为“ 非高个子 ”,且只有“女高个子”才担任“礼仪小姐”。(I)如
果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至
少有一人是“高个子”的概率是多少?(II)若从所有“高个子”中选3名志愿者,用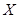 表示所
表示所
选志愿者中能担任“礼仪小姐”的人数,试写出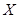 的分布列,并求
的分布列,并求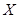 的数学期望。
的数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com