
题目列表(包括答案和解析)
如图8-3-24所示,在xOy平面内有足够大的匀强电场,电场方向竖直向上,电场强度E=40 N/C,在y轴左侧平面内有足够大的瞬时磁场,磁感应强度B1随时间t变化的规律如图乙所示,15π s后磁场消失,选定磁场垂直纸面向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3 m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8 T.t=0时刻,一质量m=8×10-4 kg\,电荷量q=2×10-4 C的微粒从x轴上xP=-0.8 m处的P点以速度v=0.12 m/s向x轴正方向入射.(g取10 m/s2,计算结果保留两位有效数字)


甲 乙
图8-3-24
(1)求微粒在第二象限运动过程中离y轴\,x轴的最大距离.
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x,y).
如图9-3-24甲所示,水平面上固定一个间距L=1 m的光滑平行金属导轨,整个导轨处在竖直方向的磁感应强度B=1 T的匀强磁场中,导轨一端接阻值R=9 Ω的电阻.导轨上有质量m=1 kg、电阻r=1 Ω、长度也为1 m的导体棒,在外力的作用下从t=0开始沿平行导轨方向运动,其速度随时间的变化规律是v=2![]() ,不计导轨电阻.求:
,不计导轨电阻.求:
(1)t=4 s时导体棒受到的安培力的大小;
(2)请在如图乙所示的坐标系中画出电流平方与时间的关系(I2-t)图象.

图9-3-24
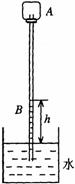 有一组同学对温度计进行专题研究。他们通过查阅资料得知十七世纪时伽利略曾设计过一个温度计,其结构为,一麦杆粗细的玻璃管,一端与一鸡蛋大小的玻璃泡相连,另一端竖直插在水槽中,并使玻璃管内吸入一段水柱。根据管中水柱高度的变化可测出相应的温度。为了研究“伽利略温度计”,同学们按照资料中的描述自制了如图所示的测温装置,图中A为一小塑料瓶,B为一吸管,通过软木塞与A连通,管的下端竖直插在大水槽中,使管内外水面有一高度差h。然后进行实验研究:
有一组同学对温度计进行专题研究。他们通过查阅资料得知十七世纪时伽利略曾设计过一个温度计,其结构为,一麦杆粗细的玻璃管,一端与一鸡蛋大小的玻璃泡相连,另一端竖直插在水槽中,并使玻璃管内吸入一段水柱。根据管中水柱高度的变化可测出相应的温度。为了研究“伽利略温度计”,同学们按照资料中的描述自制了如图所示的测温装置,图中A为一小塑料瓶,B为一吸管,通过软木塞与A连通,管的下端竖直插在大水槽中,使管内外水面有一高度差h。然后进行实验研究:
(1)在不同温度下分别测出对应的水柱高度h,记录的实验数据如下表所示
| 温度(℃) | 17 | 19 | 21 | 23 | 25 | 27 |
| h (cm) | 30.0 | 24.9 | 19.7 | 14.6 | 9.4 | 4.2 |
| △h=hn-1-hn | 2.1 | |||||
根据表中数据计算相邻两次测量水柱的高度差,并填入表内的空格。由此可得结论:
①当温度升高时,管内水柱高度h将 (填:变大,变小,不变);
②水柱高度h随温度的变化而 (填:均匀,不均匀)变化;试从理论上分析并证明结论②的正确性(提示:管内水柱产生的压强远远小于一个大气压):
。
(2)通过实验,同学们发现用“伽利略温度计”来测温度,还存在一些不足之处,其中主要的不足之处有:① ;
② 。
风力发电是目前可再生能源中技术比较成熟,具有规模化开发条件和商业发展前景的发电技术.小型独立风力发电系统一般不并网发电,只能独立使用,单台装机容量通常不超过10 KW.它的构成为:风力发电机+充电器+数字逆变器.风力发电机由机头、转体、尾翼、叶片组成.叶片用来接受风力并通过机头转为电能;尾翼使叶片始终对着来风的方向从而获得最大的风能;转体能使机头灵活地转动以实现尾翼调整方向的功能;机头的转子是永磁体,定子是绕组切割磁感线产生电能.因风量不稳定,故小型风力发电机输出的是13-25 V变化的交流电,须经充电器整流再对蓄电池充电,使风力发电机的产生的电能变能化学能.最后经逆变处理后供给用户使用.某学习小组对一小型风力发电机进行测定风速实验:将一铜棒与风力发电系统的输出端构成回路(注:风力发电机与铜棒直接相连,连接导线末画出)如图所示.铜棒ab长为0.5 m,质量0.2 Kg,两端用轻铜线相连.整个装置处在竖直向上的匀强磁场中,磁感应强度B=2 T.当有风速4 m/s吹向风叶,铜棒与竖直方向成37°角且偏向纸内的位置时,铜棒处于受力平衡状态.

(1)此时铜棒中通过的电流大小与方向.
(2)如风力发电机能把风能的30%转化为发电机的机械能,发电系统的效率为50%(其他能量损失一概不计),已知此小型风力发电系统输出电压恒定为24 V,问当铜棒与竖直方向成53°角平衡时风速为多少m/s?(g取10 m/s2,ρ空气=1.29 Kg/m3,sin37°=0.6,cos37°=0.8)
(12分)(1)以下是“探究弹力和弹簧伸长的关系”的实验步骤,按操作的先后顺序排列起来是
A.以弹簧伸长长度x 为横坐标,以弹力F为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线将点连结起来
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台置于水平桌面上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧的下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度尺上的刻度并记录在表格内,然后取下钩码
E.写出弹力随弹簧伸长量之间的变化关系
F.解释函数表达式中常数的物理意义
(2)发光晶体二极管是用电器上做指示灯用的一种电子元件.它的电路符号如图甲所示,正常使用时,带“+”号的一端接高电势,带“-”的一端接低电势.某同学用实验方法探究二极管的伏安特性曲线,现测得它两端的电压 U 和通过它的电流 I 的数据如表中所示.
| U / V | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.6 | 2.8 | 3.0 |
| I / mA | 0 | 0.9 | 2.3 | 4.3 | 6.8 | 13.0 | 19.0 | 24.0 | 30.0 | 37.0 |
① 在图乙中的虚线框内画出实验电路图.(除电源、开关、滑动变阻器外;实验用电压表V:内组 RV 约为10kΩ,电流表mA:内阻 RA 约为100Ω)
② 在图(丙)中的小方格纸上用描点法画出二极管的伏安特性曲线.
③ 根据②中画出的二极管的伏安特性曲线,简要说明发光二极管的电阻与其两端电压的关系: .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com