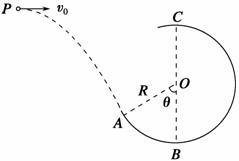
如图5－2－26所示，一个质量为0.6 kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)．已知圆弧的半径R＝0.3 m，θ＝60°，小球到达A点时的速度v_A＝4 m/s.(取g＝10 m/s²)求：

(1)小球做平抛运动的初速度v₀；

(2)P点与A点的水平距离和竖直高度；

(3)小球到达圆弧最高点C时对轨道的压力．

如图9－2－26甲所示，空间存在一宽度为2L的有界匀强磁场，磁场方向垂直纸面向里．在光滑绝缘水平面内有一边长为L的正方形金属线框，其质量m＝1 kg、电阻R＝4 Ω，在水平向左的外力F作用下，以初速度v₀＝4 m/s匀减速进入磁场，线框平面与磁场垂直，外力F大小随时间t变化的图线如图乙所示．以线框右边刚进入磁场时开始计时．

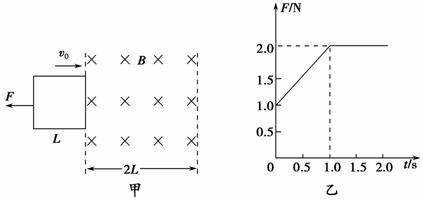
图9－2－26

(1)求匀强磁场的磁感应强度B；

(2)求线框进入磁场的过程中，通过线框的电荷量q；

(3)判断线框能否从右侧离开磁场？说明理由．

如图1－2－25所示， 波源P从平衡位置y＝0开始振动，方向竖直向上(y轴的正方向)，振动周期T＝0.01 s．产生的简谐波向右传播，波速为v＝80 m/s.经过一段时间后，S、Q两点开始振动，已知距离SP＝0.4 m、SQ＝1.0 m．若以Q点开始振动的时刻作为计时的零点，则下列说法正确的是 (　　)．

A．图1－2－26乙能正确描述Q点的振动情况

B．图1－2－26甲能正确描述S点的振动情况

C．图1－2－26丙能正确描述t＝0时刻的波形图

D．若在Q点也存在一个波源，振动情况同波源P，则S为振动加强点

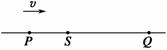
图1－2－26

如图3－4－26所示，在倾角为37°的光滑斜面上有一根长为0.4 m．质量为6×10^－2 kg的通电直导线，电流I＝1 A，方向垂直纸面向外，导线用平行于斜面的轻绳拴住不动，整个装置放在磁感应强度每秒增加0.4 T，方向竖直向上的磁场中，设t＝0，B＝0，则需要多长时间斜面对导线的支持力为零？(g取10 m/s²)

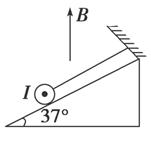
图3－4－26

 

如图11-2-26所示,有一磁感应强度B=9.1×10^－4 T的匀强磁场,C、D为垂直于磁场的同一平面内的两点,它们之间的距离l=0.05 m.今有一电子在此磁场中运动,它经过C点时的速度v的方向和磁场方向垂直,且与CD间的夹角α=30°.问:

图11-2-26

(1)电子在C点时所受的洛伦兹力的方向及大小如何?

(2)若此电子在运动中后来又经过了D点,则它的速度v应是多大?

(3)电子从C点到D点所用的时间是多少?

(电子的质量m=9.1×10^－31 kg,电子的电荷量e=1.6×10^－19 C)