
题目列表(包括答案和解析)
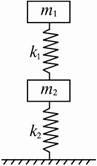
图3-2-14
? A. m1g/k1?? B. m2g/k1??
? C. m1g/k2?? D. m2g/k2??
某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,图4-2-13甲为实验装置简图(交流电的频率为50 Hz).

图4-2-13
(1)图乙为某次实验得到的纸带,根据纸带可求出小车的加速度大小为________m/s2(保留两位有效数字).
(2)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的![]() ,数据如下表:
,数据如下表:
| 实验次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/(m·s-2) | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
|
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在如图4-2-14所示的方格坐标纸中画出a-![]() 图线,并依据图线求出小车加速度a与质量倒数
图线,并依据图线求出小车加速度a与质量倒数![]() 之间的关系式是________.
之间的关系式是________.

图4-2-14

图4-2-15
(3)保持小车质量不变,改变砂和砂桶质量,该同学根据实验数据作出了加速度a随合力F的变化图线,如图4-2-15所示.该图线不通过原点,请你分析其主要原因是________________________________________________________________________
________________________________________________________________________.
图3-4-13为“验证牛顿第二定律”的实验装置示意图.砂和砂桶的总质量为m,小车和砝码的总质量为M.实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小.
(1)(单选)实验中,为了使细线对小车的拉力等于小车所受的合外力,先调节长木板一端滑轮的高度,使细线与长木板平行.接下来还需要进行的一项操作是 ( )
A.将长木板水平放置,让小车连着已经穿过打点计时器的纸带,给打点计时
器通电,调节m的大小,使小车在砂和砂桶的牵引下运动,从打出的纸带判断小车是否做匀速运动
B.将长木板的一端垫起适当的高度,让小车连着已经穿过打点计时器的纸带,
撤去砂和砂桶,给打点计时器通电,轻推小车,从打出的纸带判断小车是否做匀速运动
C.将长木板的一端垫起适当的高度,撤去纸带以及砂和砂桶,轻推小车,观
察判断小车是否做匀速运动
(2)(单选)实验中要进行质量m和M的选取,以下最合理的一组是 ( ).
A.M=200 g,m=10 g、15 g、20 g、25 g、30 g、40 g
B.M=200 g,m=20 g、40 g、60 g、80 g、100 g、120 g
C.M=400 g,m=10 g、15 g、20 g、25 g、30 g、40 g
D.M=400 g,m=20 g、40 g、60 g、80 g、100 g、120 g
(3)图3-4-14是实验中得到的一条纸带,A、B、C、D、E、F、G为7个相邻的计数点,相邻的两个计数点之间还有四个点未画出,量出相邻的计数点之间的距离分别为:sAB=4.22 cm、sBC=4.65 cm、sCD=5.08 cm、sDE=5.49 cm,sEF=5.91 cm,sFG=6.34 cm.已知打点计时器的工作频率为50 Hz,则小车的加速度大小a=________m/s2.(结果保留两位有效数字).

图3-4-13
![]()
图3-4-14
.一同学想研究电梯上升过程的运动规律.某天乘电梯上楼时他携带了一个质量为5 kg的砝码和一套便携式DIS实验系统,砝码悬挂在力传感器上.电梯从第一层开始启动,中间不间断,一直到最高层停止.在这个过程中,显示器上显示出的力随时间变化的关系如图所示.取重力加速度g=10 m/s2,根据图中的数据,求:
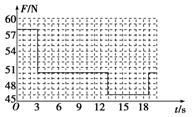
图3-6-14
(1)电梯在最初加速阶段的加速度a1与最后减速阶段的加速度a2的大小;
(2)电梯在3.0~13.0 s时间段内的速度v的大小;[来源:Zxxk.Com]
(3)电梯在19.0 s内上升的高度H.
【解析】:根据牛顿第二定律得
(1)a1== m/s2=1.6 m/s2,
a2== m/s2=0.8 m/s2.
(2)v1=a1t1=1.6×3 m/s=4.8 m/s.
(3)H=a1t+v1t2+a2t=×1.6×32 m+4.8×10 m+×0.8×62 m=7.2 m+48 m+14.4 m
=69.6 m.
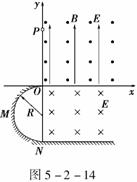
如图5-2-14所示,竖直平面坐标系xOy的第一象限,有垂直xOy平面向外的水平匀强磁场和竖直向上的匀强电场,大小分别为B 和E;第四象限有垂直xOy平面向里的水平匀强电场,大小也为E;第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道,轨道最高点与x轴相切于坐标原点O,最低点与绝缘光滑水平面相切于N.一质量为m的带电小球从y轴上(y>0)的P点沿x轴正方向进入第一象限后做圆周运动,恰好通过坐标原点O,且水平切入半圆轨道并恰好沿轨道内侧运动,过N点水平进入第四象限,并在电场中运动(已 知重力加速度为g).
(1)判断小球的带电性质并求出其所带电荷量.
(2)P点距坐标原点O至少多高?
(3)若该小球以满足(2)中OP最小值的位置和对应速度进入第一象限,通过N点开始计时,经时间t=2![]() ,小球距N点的距离s为多远?
,小球距N点的距离s为多远?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com