
题目列表(包括答案和解析)
已知函数![]()
(Ⅰ)若![]() ,求证:
,求证:![]() ;
;
(Ⅱ)是否存在实数![]() ,使方程
,使方程![]() 有四个不同的实根?若存在,求出
有四个不同的实根?若存在,求出![]() 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
设 ,若
,若 ,求证:
,求证:
(1) ;
;
(2)方程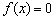 在(0,1)内有两个实根.
在(0,1)内有两个实根.
![]()
(Ⅰ)若函数f(x)在其定义域内为单调函数,求实数a的取值范围;
(Ⅱ)若函数f(x)的图像在x=1处的切线的斜率为0,且![]()
(1)若a1³3,求证:an³n+2
(2)若a1=4,试比较![]()
| 1 | n |
| PC |
| PA |
| PB |
| AP |
| AB |
| AQ |
| AC |
| 1 |
| m |
| 1 |
| n |

数 学(理科) 2009.4
一、选择题:本大题共有10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
A
C
C
B
B
二、填空题:本大题共有7小题,每小题4分,共28分.
11.
-1 12. 110 13. 78 14. 15.
15. 16. 7 17.
16. 7 17.
三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(Ⅰ)解: .……………………… 4分
.……………………… 4分
由 ,解得
,解得  .
.
所以函数 的单调递增区间为
的单调递增区间为  .…………… 7分
.…………… 7分
(Ⅱ)解:由 ,得
,得 .故
.故 .……………… 10分
.……………… 10分
于是有  ,或
,或 ,
,
即 或
或 .因
.因 ,故
,故 .……………… 14分
.……………… 14分
19.(Ⅰ)解:恰好摸到两个“心”字球的取法共有4种情形:
开心心,心开心,心心开,心心乐.
则恰好摸到2个“心”字球的概率是
 .………………………………………6分
.………………………………………6分
(Ⅱ)解: ,
,
则  ,
, ,
,
 .…………………………………………10分
.…………………………………………10分
故取球次数 的分布列为
的分布列为

1
2
3




 .…………………………………………………14分
.…………………………………………………14分
20.(Ⅰ)解:因 在底面
在底面 上的射影恰为B点,则
上的射影恰为B点,则 ⊥底面
⊥底面 .
.
所以 就是
就是 与底面
与底面 所成的角.
所成的角.
因 ,故
,故  ,
,
即 与底面
与底面 所成的角是
所成的角是 .……………………………………………3分
.……………………………………………3分
 如图,以A为原点建立空间直角坐标系,则
如图,以A为原点建立空间直角坐标系,则
 ,
,
 ,
, .
.
则 ,
,
故 与棱BC所成的角是
与棱BC所成的角是 .…………………………………………………7分
.…………………………………………………7分
(Ⅱ)解:设 ,则
,则 .于是
.于是
 (
( 舍去),
舍去),
则P为棱 的中点,其坐标为
的中点,其坐标为 .…………………………………………9分
.…………………………………………9分
设平面 的法向量为
的法向量为 ,则
,则
 ,故
,故 .…………………11分
.…………………11分
而平面 的法向量是
的法向量是 ,
,
则 ,
,
故二面角 的平面角的余弦值是
的平面角的余弦值是 .………………………………14分
.………………………………14分
21.(Ⅰ)解:由题意知: ,
, ,
, ,解得
,解得 .
.
故椭圆的方程为 .…………………………………………………5分
.…………………………………………………5分
(Ⅱ)解:设 ,
,
⑴若 轴,可设
轴,可设 ,因
,因 ,则
,则 .
.
由 ,得
,得 ,即
,即 .
.
若 轴,可设
轴,可设 ,同理可得
,同理可得 .……………………7分
.……………………7分
⑵当直线 的斜率存在且不为0时,设
的斜率存在且不为0时,设 ,
,
由 ,消去
,消去 得:
得: .
.
则 .………………………………………9分
.………………………………………9分
 .
.
由 ,知
,知 .
.
故  ,即
,即 (记为①).…………11分
(记为①).…………11分
由 ,可知直线
,可知直线 的方程为
的方程为 .
.
联立方程组 ,得
,得  (记为②).……………………13分
(记为②).……………………13分
将②代入①,化简得 .
.
综合⑴、⑵,可知点 的轨迹方程为
的轨迹方程为 .………………………15分
.………………………15分
22.(Ⅰ)证明:当 时,
时, .令
.令 ,则
,则 .
.
若 ,
, 递增;若
递增;若 ,
, 递减,
递减,
则 是
是 的极(最)大值点.于是
的极(最)大值点.于是
 ,即
,即 .故当
.故当 时,有
时,有 .………5分
.………5分
(Ⅱ)解:对 求导,得
求导,得 .
.
①若 ,
, ,则
,则 在
在 上单调递减,故
上单调递减,故 合题意.
合题意.
②若 ,
, .
.
则必须 ,故当
,故当 时,
时, 在
在 上单调递增.
上单调递增.
③若 ,
, 的对称轴
的对称轴 ,则必须
,则必须 ,
,
故当 时,
时, 在
在 上单调递减.
上单调递减.
综合上述, 的取值范围是
的取值范围是 .………………………………10分
.………………………………10分
(Ⅲ)解:令 .则问题等价于
.则问题等价于
找一个 使
使 成立,故只需满足函数的最小值
成立,故只需满足函数的最小值 即可.
即可.
因 ,
,
而 ,
,
故当 时,
时, ,
, 递减;当
递减;当 时,
时, ,
, 递增.
递增.
于是, .
.
与上述要求 相矛盾,故不存在符合条件的
相矛盾,故不存在符合条件的 .……………………15分
.……………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com