故是二面角的平面角．——青夏教育精英家教网—

故是二面角的平面角．【查看更多】

题目列表(包括答案和解析)

如图，在正三棱柱ABC-A₁B₁C₁中，E∈BB₁，截面A₁EC⊥侧面AC₁．

（1）求证：BE=EB₁；
（2）若AA₁=A₁B₁；求平面A₁EC与平面A₁B₁C₁所成二面角（锐角）的度数．
注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．

（1）证明：在截面A₁EC内，过E作EG⊥A₁C，G是垂足．
①∵

∴EG⊥侧面AC₁；取AC的中点F，连接BF，FG，由AB=BC得BF⊥AC，
②∵

∴BF⊥侧面AC₁；得BF∥EG，BF、EG确定一个平面，交侧面AC₁于FG．
③∵

∴BE∥FG，四边形BEGF是平行四边形，BE=FG，
④∵

∴FG∥AA₁，△AA₁C∽△FGC，
⑤∵

∴FG=

AA1=

BB1，即BE=

BB1，故BE=EB1．

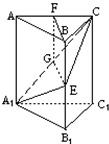
如图，四棱锥S—ABCD中，SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB

(Ⅰ)证明：平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .

【解析】本试题主要考查了立体几何中的运用。

(1)证明：因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.，因此可知得到平面EDC⊥平面SBC.

（Ⅱ）由SA²= SD²+AD² = 5 ，AB=1，SE=2EB，AB⊥SA，知

AE²= (1 /3 SA)²+(2/ 3 AB)² =1，又AD=1．

故△ADE为等腰三角形．

取ED中点F，连接AF，则AF⊥DE，AF²= AD²-DF²=．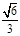

连接FG，则FG∥EC，FG⊥DE．

所以，∠AFG是二面角A-DE-C的平面角．

连接AG，AG= 2 ，FG²= DG²-DF² =，

cos∠AFG=(AF²+FG²-AG² )/2⋅AF⋅FG =-1 /2 ，

所以，二面角A-DE-C的大小为120°

下面推理是类比推理的是（）

A．两条直线平行，则同旁内角互补，若∠A和∠B是同旁内角，则∠A＋∠B＝180°

B．由平面三角形的性质，推测空间四边形的性质

C．某校高二有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此推测各班都超过50位团员

D．一

切偶数能被2整除，2¹⁰⁰是偶数，故2¹⁰⁰能被2整数

下面推

理是类比推理的是（）

A．两条直线平行，则同旁内角互补，若∠A和∠B是同旁内角，则∠A＋∠B＝180°

B．由平面三角形的性质，推测空间四边形的性质

C．某校高二有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此推测各班都超过50位团员

D．一

切偶数能被2整除，2¹⁰⁰是偶数，故2¹⁰⁰能被2整数

同步练习册答案