
题目列表(包括答案和解析)
(本题满分14分)在等差数列 中,
中, ,其前
,其前 项和为
项和为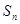 ,等比数列
,等比数列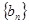 的各项均为正数,
的各项均为正数, ,公比为
,公比为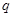 ,且
,且 ,
,
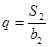 .
.
(Ⅰ)求 与
与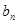 ;(Ⅱ)证明:
;(Ⅱ)证明: ≤
≤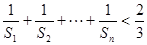 .
.
(本题满分14分)在等差数列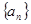 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列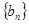 的各项均为正数,
的各项均为正数, ,公比为
,公比为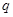 ,且
,且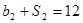 ,
,  .
.
(Ⅰ)求 与
与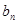 ;(Ⅱ)证明:
;(Ⅱ)证明: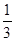 ≤
≤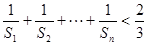 .
.
 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
,  .
. 与
与 ;(Ⅱ)证明:
;(Ⅱ)证明: ≤
≤ .
. (本题满分14分)在数列![]() 中,已知
中,已知![]() .
.
(1)证明数列![]() 是等比数列;(2)
是等比数列;(2) ![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() 的表达式;
的表达式;
(3)在(2)的条件下,若存在自然数![]() 使
使![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
(本题满分14分) 在 中,角
中,角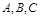 所对的边分别为
所对的边分别为 ,已知
,已知 成等比数列,且
成等比数列,且 .
.
(Ⅰ)求角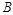 的大小;
的大小;
(Ⅱ)若 ,求函数
,求函数 的值域.
的值域.
|