
题目列表(包括答案和解析)
(本题满分15分) 在直角坐标系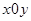 中,点
中,点 到两点
到两点 、
、 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为曲线
的轨迹为曲线 ,直线
,直线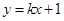 与曲线
与曲线 交于
交于 、
、 两点.
两点.
(1)求出 的方程;
的方程;
(2)若 =1,求
=1,求 的面积
的面积
(3)若OA⊥OB,求实数 的值
的值
(本题满分15分) 在直角坐标系 中,点
中,点 到两点
到两点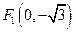 、
、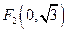 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为曲线
的轨迹为曲线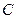 ,直线
,直线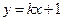 与曲线
与曲线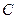 交于
交于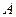 、
、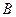 两点.
两点.
(1)求出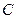 的方程;
的方程;
(2)若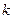 =1,求
=1,求 的面积
的面积
(3)若OA⊥OB,求实数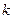 的值
的值
(本小题满分10分)以直角坐标系的原点O为极点,x轴的正半轴为极轴.
已知点P的直角坐标为(1,-5),点M的极坐标为(4,).若直线l过点P,
且倾斜角为 ![]() ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.
(I)求直线l关于![]() 的参数方程(其中
的参数方程(其中![]() 表示有向线段
表示有向线段![]() 的数量,
的数量,![]() 为直线l上
为直线l上
任意一点)和圆C的极坐标方程;
(II)试判定直线l和圆C的位置关系.
| MO |
| ME |
| MO |
| ME |
|